Ball on Wheel

Golyó a keréken

Ver240104a

https://konf2023.kvk.uni-obuda.hu/publikaciok

VID_20230913_210931.3gp

Dobány Imre, Dr. Kopják József

Dobány Imre, Kandó Kálmán Villamosmérnöki Kar, Óbudai Egyetem, 1034 Budapest, Bécsi út 94-96., imre@dobany.hu

Absztrakt: https://konf2023.kvk.uni-obuda.hu/absztraktok

A „golyó a keréken” problémában egy golyót kell egyensúlyozni a biciklikerék tetején. Ez egy általános iskolapélda az irányítástechnika szakterületén [1], hasonlóan a jól ismert „fordított inga” vagy a „reaction wheel” problémákhoz.

A SISO szabályozás bemente a golyó pozíció, kimenete a motor feszültség. A modell alkotás Newton és Lagrange módszerrel készült, amelyek után a motor paraméter identifikáció és a szabályozó tervezés követte PID, állapot visszacsatolás, állapot becslővel és LQ [2] szabályozókkal Scilab, Xcos és Octave-CLI fejlesztőkörnyezetben. A motorhoz HALL szenzoros hajtás került megvalósításra Arduino-CLI-Nano fejlesztő környezetben. Mivel a legegyszerűbb, legköltséghatékonyabb oktatási összeállításra törekedtem, ezért Linux-os operációs rendszeren, akár PC-n vagy például Raspberry PI számítógép platformon futtatható a szabályozó Octave szkript. A számítógép UART interfészen kommunikál az Arduino Nano kártyával, ahol analóg pozíció érzékelés történik Tsample = 20-100msec időzítéssel, amit a Linux delegált CPU-core-ja elegendő pontossággal kiszolgál. Az Arduino végzi a BLDC motor hajtást a kapott motor kapocsfeszültség alapján.

Az összeállítással megmutatható a modellalkotás, motor paraméter identifikáció, szabályozó tervezés menete, továbbá vizsgálható a szabályozók érzékenysége és robusztussága.

Kulcsszavak: Newton modell, Lagrange modell, instabil szabályozás, állapotvisszacsatolás, LQ szabályozó

A cikk célja, hogy megmutasson egy automatizálási feladat megoldást a kezdetektől a fizikai megvalósításig modern, de a végletekig leegyszerűsített anyagi erőforrást igénylő eszközökkel, ily módon alkalmassá téve a mindenki számára hozzáférhető oktatási demonstrációs eszközként.

Először a kísérleti elrendezés és a rendszer fizikai tulajdonságai 19kerülnek röviden bemutatásra, amelyek a későbbi szabályozó tervezéshez szükségesek. Ezt követi a modellalkotás Newton és Lagrange módszerrel a fizikai tanulmányok iskola példájaként.

A rendszer modell linearizálása után a szabályozó tervezés bemutatása követi, amelyben a manapság használatos programokkal elvégezhető matematikai műveletsorok kerülnek bemutatásra, míg a mélyebb magyarázatot a megjelölt irodalomjegyzékben megtalálhatjuk. A következő fejezetekben a szabályozó megvalósítás valamint golyó pozíció érzékelés és beavatkozáshoz szükséges motor hajtás kerül megemlítésre.

A cikk végén a szabályozó tervezéshez szükséges fizikai paraméterek meghatározásához (paraméter identifikáció) szükséges lépések kerülnek bemutatásra.

Az összeállítás továbbfejlesztési lehetőségeket rejt magában, mint például felhasználói böngészőn keresztüli html interfész kialakítását, ahol szabályozó típust (PID, állapotvisszacsatolás, LQ), mintavételi időt, jittert, alapjelet, stb. lenne lehetőség állítani, így vizsgáhatóvá válna a különböző szabályozók érzékenység és robosztusságának vizsgálatára. Az eszköz valamely egyszerűsített, lekicsinyített másolata alkalmas lehet csináld magad (DIY) egységcsomag kialakítására, amely motiváló lehet a tanulók számára.

Az összeállításról videó elérhető az alábbi linken: https://drive.google.com/file/d/1aYekoKIV0XY-9lRHnn9m6GJVegpmdNTa/view?usp=drive_link

Röviden ismertetem a ’golyó a keréken’ rendszert, amely egy általánosan ismert irányítástechnikai iskolapélda. Leegyszerűsítve arról van szó, hogy egy kerék tetején kell egy golyót egyensúlyozni, ahol beavatkozó szerv egy kereket hajtó motor, lásd az alábbi ábra.

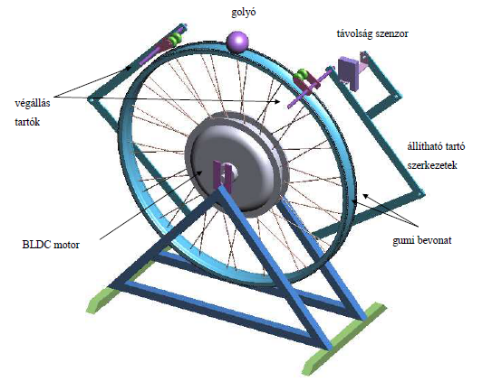
Esetemben egy elektromos kerékpár 22 col-os tömlő nélküli felni gumival bevont peremein gurul egy biliárdgolyó. A kereket BLDC motor hajtja, hall szenzorokkal ellátva. A golyó pozícióját lézeres távolságmérővel mérem. Az így kialakult rendszer egy egydimenziós kényszerpályán mozgó golyó, aminek gyakorlatilag nincs egyensúlyi pontja, ezért csak instabil pozícióra tudunk szabályozni vagy egy trajektória mentén irányítani a rendszert, ha a rendszer irányítható és mivel csak a golyó pozíciót mérem, ezért a rendszer belső állapotainak megállapításához becslőt kell használni, amennyiben a rendszer matematikailag megfigyelhető.

Matematikai lineáris modellre van szükségünk, hogy a szabályozót meg tudjuk valósítani. Fizikában a mechanika és az elektrodinamika területén a Newton és Lagrange modellezés használatos.

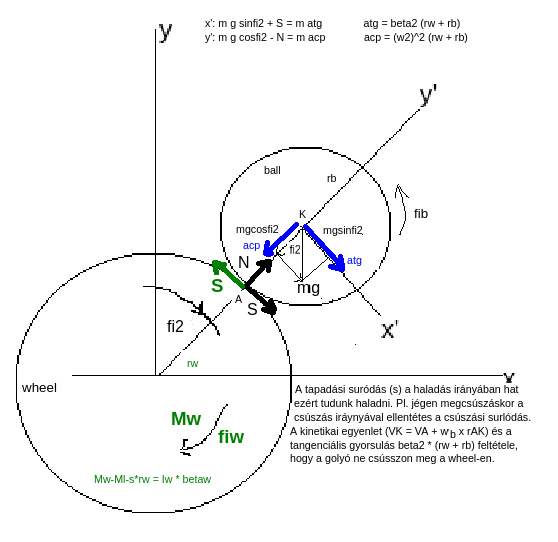
2-1. ábra Golyó a keréken rendszermodell [1]

Paraméterek és jelölések

2-1. táblázat Terminológia és paraméterek

2.2.1 Kinetikai feltételek

A modellhez elengedhetetlen, hogy a golyó a keréken ne csússzon meg, azaz a tapadás mindvégig fennálljon, ami a tiszta gördülés esetét jelenti. Ekkor a találkozási pont nyugalomban van, nincs relatív elmozdulás, tehát úgy modellezhető, mintha a golyó és a kerék össze lenne ragasztva. Más kérdés, hogy a golyó közben forog a kerületén ható erő miatt, ami majd forgató nyomatékot okoz. Ezen ok miatt az (AN.1.) használható.

2-2. ábra Kinetikai feltétel

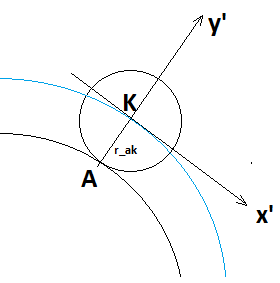
A golyó (Vk) tömegközéppontjának transzlációs (VA) és rotációs (wb x rAK) mozgása közötti kapcsolatot az alábbi egyenlettel fejezhetjük ki. [10]

(AN.1.)

(AN.2.)

(AN.5.)

A tiszta gördülés, tapadás addig áll fenn, amíg a tapadási erő kisebb vagy egyenlő, mint a súrlódási erő.

(AN.6)

A μ értékét az anyagok közötti tulajdonságok határozzák meg. A fenti azonosságot tapasztalati úton fogom ellenőrizni. A differenciálegyenlet felírásához, majd, mint látni fogjuk közvetlenül erre nincs szükség.

2.2.2 Mozgásegyenletek-golyóra

A golyó mozgás egyenletének felírásakor kísérő-triéderes koordináta rendszert használok a 2-1. ábra szerint (x’; y’).

Egy tömegközéppontra 6 mozgásegyenletet tudunk felírni:

• 3-at, (x; y; z) irányban a transzlációs mozgásra és

• 3-at, (x₂; y₂; z₂) irányban a rotációs mozgásra.

Jelen esetben, mivel sík problémáról van szó

• 2 db egyenlet a transzlációs mozgásról szól (x; y)

• 1 db egyenlet a rotációs, forgómozgásról szól (z₂)

transzlációs egyenletek

(AN.7) (AN.9)

(AN.8) (AN.10)

rotációs egyenlet

(AN.11)

2.2.3 Mozgásegyenletek - kerékre

A kerék koordináta rendszerét az 2-1. ábra szerint választom. Mivel transzlációs mozgást nem végez a kerék, ezért egyenletei sincsenek. Mivel a kerék forog, ezért rotációs egyenlete van.

(AN.12)

Az ‘M’ nyomatékba a motor csapágy súrlódást (M_L) negatív előjellel a későbbiekben bele kell számolni.

(AN.13)

és (AN.14)

2.2.4 Összevont mozgásegyenletek

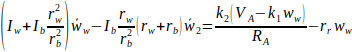(AN.15)

(AN.16)

Az egyenletrendezés például Octave, Sympy, Matlab és Maxima programokkal is megoldhatóak.

2.3 Modell Lagrange szerint

A Lagrange modell szerint a szakasz Lagrange függvénye [1][2]

(AL.1)

ahol ’T’ a mozgási energia és ’V’ a helyzeti energia, ’L’ pedig a Lagrange-függvény.

Esetünkben tehát:

(AL.2) – kerék mozgási energiája

(AL.3) – Golyó mozgási energiája

(AL.4) – Golyó helyzeti energiája

(AL.5)

(AL.9)

Így a Lagrange változók:

(AL.10)

A Lagrange-egyenlet nem konzervatív rendszer esetén:

(AL.12)

ahol a nem konzervatív erőkből álló általános erők eredője.

Tehát a feladat (AL.9) egyenlet (AL.12) egyeletbe helyettesítése és megoldása. Az (AL.12) egy egyenletrendszer, amelyben Qi*( ; ).

(AL.13), a motor modell alapján,

(AL.14), a pozíciónak nincs általános ereje. A motor modelljében ( az armatúra áram dinamikája elhanyagolásra került.

2.3.1 Lagrange parciális derivált szerint.

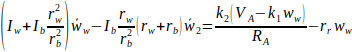(AL.15)

2.3.2 Lagrange parciális derivált szerint.

(AL.16)

2.4 Newton Lagrange modell azonosság

Az (AN15), (AN.16) és (AL15), (AL.16) egyenleteket páronként összehasonlítva, látható, hogy az egyenletek megegyeznek, tehát igazoltuk, hogy a különböző modellek azonos eredményt adnak.

2.4.1 Octave

#script

pkg load symbolic

clear

syms t

syms fib fiw fi2 omegab betab omegaw betaw omega2 beta2

syms mb g N s rb rw rv km ku Ua Ra thetab thetaw murelative

syms x y z

#kinematika

vbc_m = [[(rw + rb) * omega2]; [0]; [0]]

vp_m = [[rw * omegaw]; [0]; [0]]

omegab_m = [[0]; [0]; [omegab]]

rb_m = [[0]; [rb]; [0]]

#s <= murelative * N # not used

#dinamika

#dinamika golyo

acp = omega2^2*(rw+rb) # not used

mb * g * cos(fi2) - N == mb * acp # not used

atg = beta2*(rw+rb)

#dinamika kerek

Mm = km*(Ua-ku*omegaw)/Ra

Ms = rv*omegaw

#---------------------

kzzz=(vp_m + cross(omegab_m, rb_m))

sol_omegab = solve(vbc_m(1) == kzzz(1), omegab)

betab = (-beta2*rb - beta2*rw + betaw*rw) / rb

sol_s = solve(s * rb == thetab * betab, s)

equs=[

mb * g + sol_s == mb * atg;

Mm - Ms - sol_s * rw == thetaw * betaw;

]

equs_sol=solve(equs, beta2, betaw)

equs_sol

#eof

#outputs

>> bow_v2

Symbolic pkg v3.1.1: Python communication link active, SymPy v1.10.1.

vbc_m = (sym 3x1 matrix)

[omega2*(rb + rw)]

[ ]

[ 0 ]

[ ]

[ 0 ]

vp_m = (sym 3x1 matrix)

[omegaw*rw]

[ ]

[ 0 ]

[ ]

[ 0 ]

omegab_m = (sym 3x1 matrix)

[ 0 ]

[ ]

[ 0 ]

[ ]

[omegab]

rb_m = (sym 3x1 matrix)

[0 ]

[ ]

[rb]

[ ]

[0 ]

acp = (sym)

2

omega2 *(rb + rw)

ans = (sym)

2

-N + g*mb*cos(fi2) = mb*omega2 *(rb + rw)

atg = (sym) beta2*(rb + rw)

Mm = (sym)

km*(Ua - ku*omegaw)

-------------------

Ra

Ms = (sym) omegaw*rv

kzzz = (sym 3x1 matrix)

[-omegab*rb + omegaw*rw]

[ ]

[ 0 ]

[ ]

[ 0 ]

sol_omegab = (sym)

-omega2*rb - omega2*rw + omegaw*rw

----------------------------------

rb

betab = (sym)

-beta2*rb - beta2*rw + betaw*rw

-------------------------------

rb

sol_s = (sym)

-beta2*rb*thetab - beta2*rw*thetab + betaw*rw*thetab

----------------------------------------------------

2

rb

equs = (sym 2x1 matrix)

[ -beta2*rb*thetab - beta2*rw*thetab + betaw*rw*thetab ]

[ g*mb + ---------------------------------------------------- = beta2*mb*(rb + rw) ]

[ 2 ]

[ rb ]

[ ]

[ rw*(-beta2*rb*thetab - beta2*rw*thetab + betaw*rw*thetab) km*(Ua - ku*omegaw) ]

[-omegaw*rv - --------------------------------------------------------- + ------------------- = betaw*thetaw]

[ 2 Ra ]

[ rb ]

equs_sol =

scalar structure containing the fields:

beta2 =

<class sym>

betaw =

<class sym>

equs_sol =

scalar structure containing the fields:

beta2 =

<class sym>

betaw =

<class sym>

2.4.2 Sympy

A számolást Sympy programmal is elvégzem. A Raspberry Pi Zero 2w, Debian rendszerre:

imre@raspberrypi:~ $ sudo apt-get install python3-pip

git clone https://github.com/sympy/sympy.git

git pull origin master

python -m pip install -e .

imre@raspberrypi:~ $ python ./bowSymbol.py

Python 3.9.2 (default, Feb 28 2021, 17:03:44)

# sudo apt-get install python

# sudo apt-get install python3-pip

# python .\bow.py

from sympy import *

import sympy as sp

import sympy

print("Hello, World!")

print(sympy.__version__)

#golyo kinematika

rw, rb, omega2, omegaw, omegab = symbols('rw rb omega2 omegaw omegab')

vbc_m = Matrix([[(rw + rb) * omega2], [0], [0]])

#print(vbc_m[0])

vp_m = Matrix([[rw * omegaw], [0], [0]])

omegab_m = Matrix([[0], [0], [omegab]])

rb_m = Matrix([[0], [rb], [0]])

eq_kin1 = Eq(vbc_m[0], (vp_m + omegab_m.cross(rb_m))[0])

eq_kin1 = simplify(eq_kin1)

print(eq_kin1)

print("ezt kene automatan kifejezni, ha omegara igaz, akkor beta-ra is…")

#Eq(omega2*(rb + rw), -omegab*rb + omegaw*rw)

beta2, betaw, betab = symbols('beta2 betaw betab')

eq_kin2 = Eq(beta2*(rb + rw), -betab*rb + betaw*rw)

print(eq_kin2)

#sol_beta2 = solve(eq_kin2, beta2)

#print(sol_beta2)

#golyo dinamika

m, g, fi2, N, S, jb = symbols('m g fi2 N S jb')

acp = omega2**2*(rw+rb)

eq_dinb1 = Eq(m*g*cos(fi2)-N, m*acp)

print(eq_dinb1)

atg = beta2*(rw+rb)

eq_dinb2 = Eq(m*g*sin(fi2)+S, m*atg)

print(eq_dinb2)

eq_dinb3 = Eq(S * rb, jb * betab)

print(eq_dinb3)

#kerek dinamika

u, ke, ki, Ra = symbols('u ke ki Ra')

Mw, Ml, jw, FF = symbols('Mw Ml jw FF')

Mw = ki*(u-ke*omegaw)/Ra

Ml = FF*omegaw

eq_dinw1 = Eq(Mw - Ml - S*rw, jw*betaw)

print(eq_dinw1)

#https://docs.sympy.org/latest/guides/solving/solve-system-of-equations-algebraically.html

#Equations Which Have a Closed-Form Solution, and SymPy Cannot Solve

#https://stackoverflow.com/questions/31547657/how-can-i-solve-system-of-linear-equations-in-sympy

#sol = solve([eq_kin1, eq_kin2, eq_dinb1, eq_dinb2, eq_dinb3, eq_dinw1], [beta2], dict=True)

sol = sp.solve((eq_kin1, eq_kin2, eq_dinb2, eq_dinb3, eq_dinw1), beta2, dict=True)

print(sol)

#answer: [] <----csak egy ures struktura...ugyenez jon octave-ban

#outputs

#Hello, World!

#1.9

#Eq(omega2*(rb + rw), -omegab*rb + omegaw*rw)

#ezt kene automatan kifejezni

#Eq(beta2*(rb + rw), -betab*rb + betaw*rw)

#Eq(-N + g*m*cos(fi2), m*omega2**2*(rb + rw))

#Eq(S + g*m*sin(fi2), beta2*m*(rb + rw))

#Eq(S*rb, betab*jb)

#Eq(-FF*omegaw - S*rw + ki*(-ke*omegaw + u)/Ra, betaw*jw)

#[]

2.4.3 Matlab

#script ugyanaz,mint Octave

#output

beta2

val =

(Ua*km*rw*thetab - Ra*omegaw*rv*rw*thetab - km*ku*omegaw*rw*thetab + Ra*g*mb*rb^2*thetaw*sin(fi2) + Ra*g*mb*rw^2*thetab*sin(fi2))

/(Ra*(rb + rw)*(mb*thetaw*rb^2 + mb*thetab*rw^2 + thetab*thetaw))

betaw

val =

-(Ra*omegaw*rv*thetab - Ua*km*thetab + km*ku*omegaw*thetab - Ua*km*mb*rb^2 + Ra*mb*omegaw*rb^2*rv + km*ku*mb*omegaw*rb^2 - Ra*g*mb*rw*thetab*sin(fi2))

/(Ra*(mb*thetaw*rb^2 + mb*thetab*rw^2 + thetab*thetaw))

2.4.4 Maxima

A számolást a Maxima programmal is elvégzem és összehasonlítást végzek a Sympy prgrammal.

>sudo apt-get install maxima

>maxima

(%i1)batch(“bow240108a.mc”)

2.5 Differenciális egyenletrendszer

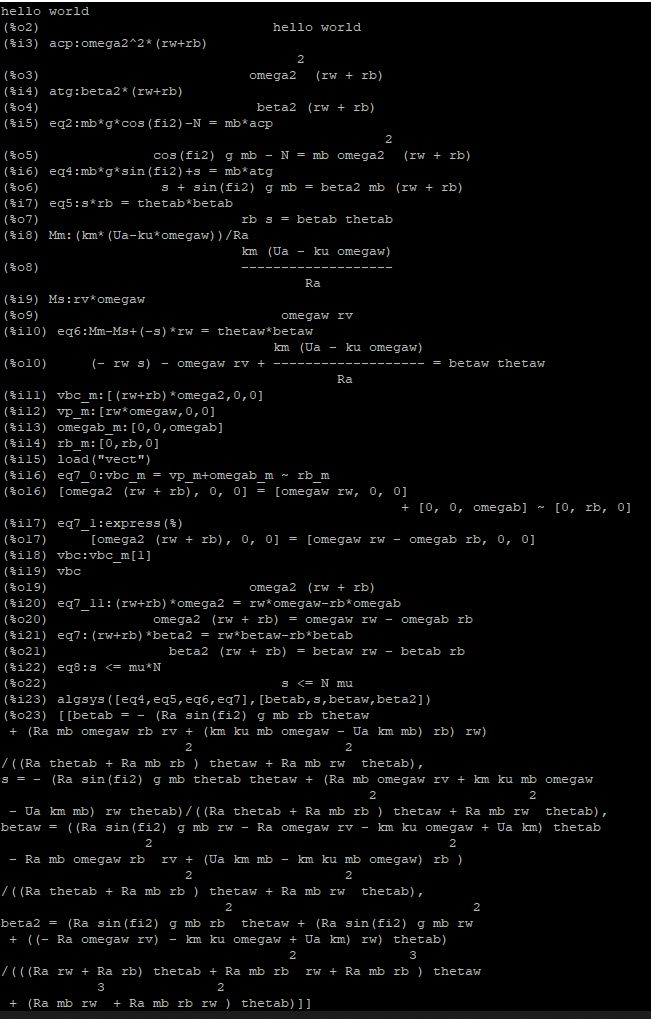
Az rendszeregyenlethez a konstansokra egyszerűbb jelölést bevezetve:

(AE.1)

(AE.2)

(AE.3)

Ahol ; ; ;

; ; .

*****************

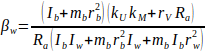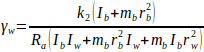Az x=fx+g(x)UA  rendszeregyenlethez a konstansokra egyszerűbb jelölést bevezetve:

ww=(wsin 2 -www)+wUa (AE.1)

w2=(2sin 2 -2ww)+2Ua (AE.2)

2=w2       (AE.3)

Ahol w=IbrwmbgIbIw+mbrb2Iw+mbIbrw2;w=Ib+mbrb2kUkM+rVRaRaIbIw+mbrb2Iw+mbIbrw2 ;w=k2Ib+mbrb2RaIbIw+mbrb2Iw+mbIbrw2 ;

2=Iwrb2+Ibrw2rw+rbIbIw+mbrb2Iw+mbIbrw2 ;2=IbrwkUkM+RarrRArw+rbIbIw+mbrb2Iw+mbIbrw2 ;2=IbrwkMRarw+rbIbIw+mbrb2Iw+mbIbrw2 .

A feladat, hogy az x=fx+g(x)∙UA🡪 linearizálás 🡪 x=Ax+b UA

ahol A=∂f∂x |Xe,UA és b=∂gUA |Xe,UA. Az Xeaz egyensúlyi helyzethez tartozó paramétereket tartalmazza, A rendszermátrix és b konstans vektor, ami a bemeneti UA paraméteren keresztül hat. Ennek érdekében az egyensúlyi pont körül linearizálást végzünk. A linearizálás során az egyensúlyi helyzet körül, amikor az x=0 megvalósul, a nem lineáris sin 2 ~=2  lineáris taggal közelítjük, ami 5 fokig gyakorlatban megfelelő.

fxxe=f1ww f1w2 f12; f2ww f2w2 f22; f3ww f3w2 f32 xe

=w2-wwwww w2-wwww2 w2-www2; 22-2wwww 22-2www2 22-2ww2; w2ww w2w2 w22

Tehát az x=Ax+b UA egyenlet az alábbiak szerint alakul:

ww; w2; 2 =-w 0 w; -2 0 2; 0 1 0 ww; w2; 2 +w; 2; 0 UA

 CT= (0; 0;1)

D= 0

Így kialakult az állapotteres szakasz modell.

Ábra 2.3-1

Állapotteres modell [3]

2.5.1 Symbolic Tools Összehasonlítás

A symbolic tool-ok használatát izgalmas volt kipbálni, amire nekem szuksegem volt az csak a “Solve a System of Equations Algebraically” feladat. Nem volt szukseg numerikus megoldasra. Egyertelmuen a Maxima a legrobosztusabb, jollehet a legregebbi. Az Octave a Sympy-t hasznalja, ,ezert uaz az eredmenyt adja. Jo lenne megoldani, hogy a szimbolikus modell alkotas utan autoatikusan atterhtnenk a allapotteres linspace modell alkotasra (ss(A,B,C,D)) es LQ szabylozo tervezesre. Ehhez ket problemat kene megoldani: 1, a symbolumok derivaltjaval is tudjon a solve() dolgozni, valamint, hogy az Octave, sympy solve() is mukodjon. Ezt meg nem sikerult elernem.

3. Szabályozó tervezés

A szabályozó tervezést a szakasz vizsgálatával szükségszerű kezdeni.

3.1 Szakasz vizsgálat

Részlettörtes alakra alakítást például Matlab program segítségével is végezhetjük, ‘zpk(bow_sys)’ függvény hívással:

                   8.5542 s

      -----------------------------         (3.1)

  (s+56.44) (s+3.278) (s-3.282)

Látható, hogy van egy jobb oldali labilis, nem lengő pólus és egy jobb oldali kicsi nem lengő zérus, ami nem minimálfázisú rendszert jelent, tehát a bemeneti jel hatására lassú elszálló jelleget mutat a rendszer, ami egy késleltetést jelent. 

A szakasz a Scilab ‘rank’ függvénnyel vizsgálva irányíthatónak és megfigyelhetőnek bizonyult [3].

AB = [B, A*B, A*A*B;] #irányíthatósági mátrix

--> rank(AB)

 ans  =   3. #irányítható a rendszer

--> CA=[C; C*A; C*A*A;]

--> rank(CA)

 ans  = 3. #megfigyelhető

3.2 Tervezési sarokpontok

A tervezésnél szempont az alacsony költség és az alkatrészek beszerezhetősége. Ezért már most kialakulnak sarokpontok:

• Szabad felhasználású licensz, alacsony árú, egyszerű HW, például Arduino Nano + inverter: BTS7960-M, UART, Ts = 20-100msec,

• Maximum kilengés < 5fok,

• 6step hajtás, 1 szektor-12.6 mm fent a kerék tetején 2.5fok,

• TpositionADC = 2.5msec,

• Tszakasz = 100msec,

• Linux használat, softRT, Scilab, Octave az egyszerű kontroller implementacio érdekében lehet PC vagy SoC, pl Raspberry Zero 2W.

A fentiek figyelembe vételével a szakasz vizsgálatot követően a szabályozó paraméterek számítását hangolását, majd szimulációját Scilab, Xcos és Matlab programmal végeztem. 

3.3 PID szabályozó

Mivel jobb oldali zérus van, azt polinom kiejtessel nem hasznos kiejteni, mert megmarad a belső instabilitás (nem irányítható, nem megfigyelhető)[3].

Tehát el kell fogadni a jobb oldali zérus által okozott ellentétes kilengést (minimálfázisú) és késleltetést. Mivel ez kicsi a szakasznál, e-14 nagyságrendű, lehet vele próbálkozni a gyakorlatban.

A jobb oldali labilis pólus kezelése [3], pólus kiejtés zérussal nem szabad, mert megmarad a strukturális instabilitás (nem megfigyelhető, nem irányíthatóvá válik). A szabályozó és szakasz nyílt hurkú Nyquist görbének az óra járásával ellentétesen kell 1-szer (1 jobb oldali pólus esetén) kerülnie -1-et. A PID szabályozó ideális paramétereit a Matlab program segítségével könnyen megtalálhatjuk. 

>> Gd = c2d(sys, Ts);       % Create discrete-time plant

>> pidTuner(Gd, 'pid')

 Cpid_discr =

                           1                1

  Kp + Ki * Ts * ------ + Kd * ----- * z-1

                          z-1              Ts 

   with Kp = 534, Ki = 5.14e+03, Kd = 12.1, Ts = 0.02

Sample time: 0.02 seconds

Discrete-time PID controller in parallel form.

Ábra 3-1

Nyquist diagramm, PID szabályozó és szakasz, nyílt hurok

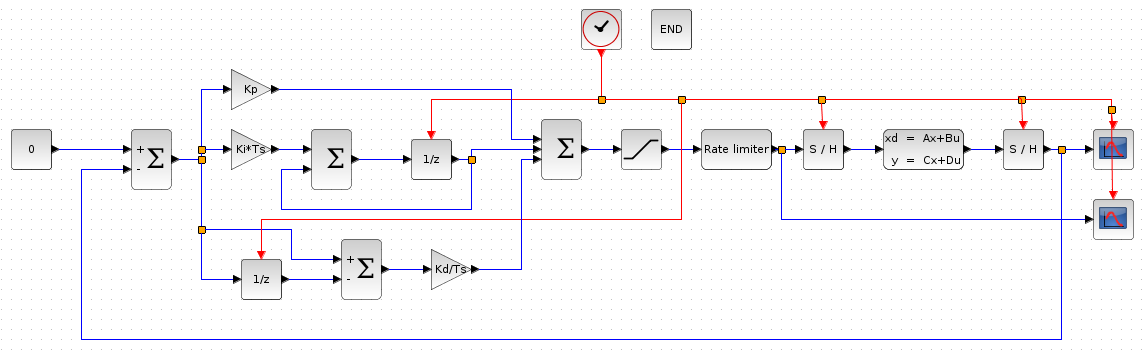
Ábra 3-2

PID szabályozó szimulációs blokkvázlat

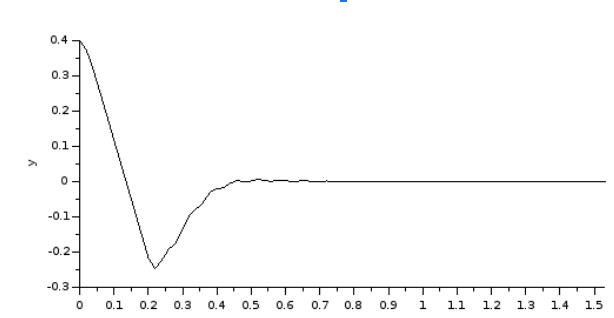
Ábra 3-3

PID szabályozó, pozíció idő függvény

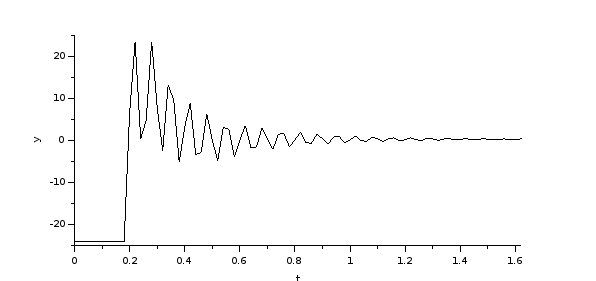
Ábra 3-4

PID szabályozó, motor feszültség

3.4 Állapot visszacsatolás

A szakasz diszkretizáció [3], amit például az Octave [7] programmal végezhetünk: 

BoW_ssd=c2d(BoW_ss, Ts);

,ahol Ts a mintavételi idő.

Állapot visszacsatolás [3]

A visszacsatoló kT vektor meghatározása pólusáthelyezéses iterációval végezhető [3], amire most a cikk nem tér ki. Egy másik lehetőség az LQ algoritmus [3][4] alkalmazása, ahol lineáris vektor térben keressük a bemenet és a kimenet közötti optimumot paraméter súlyozással, költség függvénnyel. A súlyok meghatározása iterációs feladat, de jellegében a (3.2) szerint alakul [12].

        (3.2)

q1 = 0.009118906527810399; #omegaw súly

q2 = 0.0914991210900477; #omega2 súly

q3 = 131.3122540004697; #fi2 súly

R = 0.25; #Uk súly

Q = diag([q1, q2,q3]);

Big = blkdiag(Q,R);         #közös nagy Q R matrix

#// Now we calculate C1 and D12

nstates = 3;

[w,wp] = fullrf(Big); #[5]

C1=wp(:,1:nstates); #kiválasztjuk az összes sort és az 1->nstates oszlopokat

D12=wp(:,end);   #[C1,D12]'*[C1,D12]=Big //mindegyik sor utolsó eleme-->oszlop matrix

P = ss(A,B,C1,D12);   #foly. idejű szakasz

[Kd,X] = lqr(P, Q, R);

Tehát a szabályozó a Kd vektor visszacsatoló tagból áll.

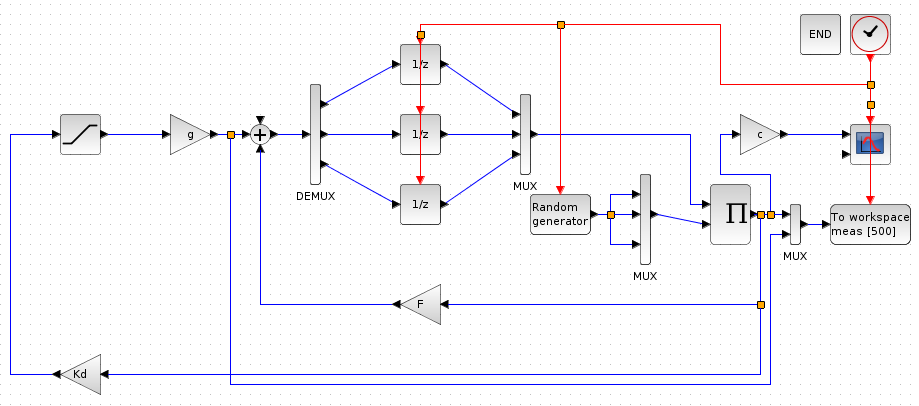
Ábra 3.4-1

Állapot visszacsatolás

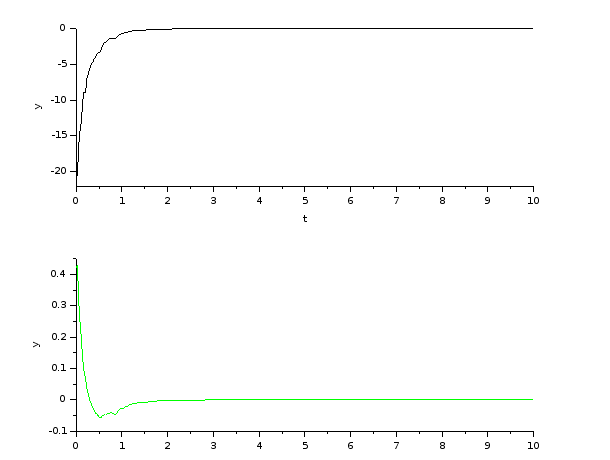
Ábra 3.4-2

Állapot visszacsatolás, szimuláció idő diagram

3.5 Állapot becslő

Az állapot visszacsatolás akkor működik, ha az állapot változókat vissza tudjuk mérni, azonban legtöbbször nem ez a helyzet, mint ahogy ebben az esetben sem. Csak a golyó pozícióról van információnk, viszont mivel ismerjük a rendszer modellt, ezért lehetőség van megbecsülni a többi állapot változót [3][4]. 

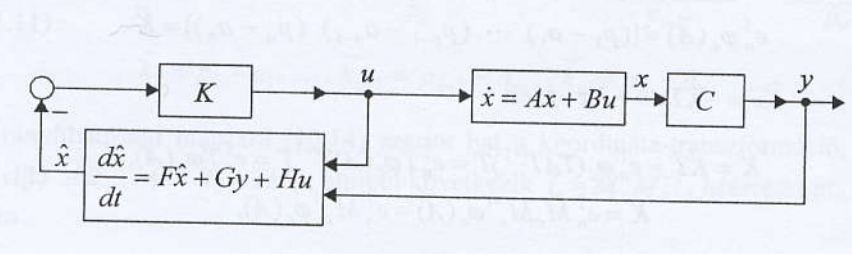
Ábra 3.5-1

Állapot becslő [4]

A becslő a szakasz modell egy másolata, amire szintén lehet az LQ eljárást alkalmazni.

FT = F';

cT = c';

Big_est = blkdiag(Q,R);      

[w_est, wp_est] = fullrf(Big_est);

c1_est = wp_est(:,1:nstates); 

d12_est = wp_est(:,end);  

P_est = ss(FT, cT, c1_est, d12_est, Ts);

[K_estd,X_estd] = lqr(P_est, Q, R);

eFTcTKestd=eig(FT+cT*K_estd);                        

Gd = K_estd';

Fd = F - Gd * c;

Hd = g;

Tehát a szabályozó:

 sum_zn1 = Fd * sum_zn1 + Gd * x(3) + Hd * u;

 u = Kd * sum_zn1;

Ahol ‘x(3)’ a mért golyó pozíció, ‘u’ pedig a kiadott motor kapocsfeszültség.

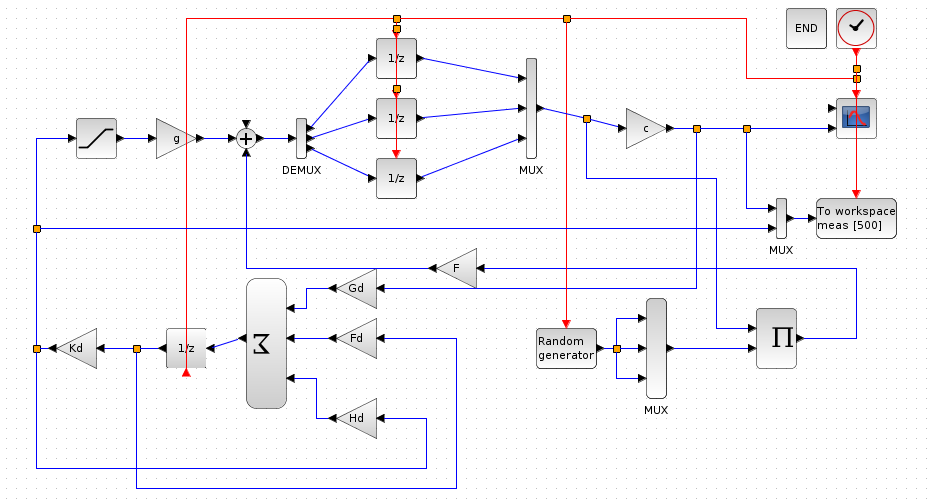
Ábra 3.5-2

Állapot becslő

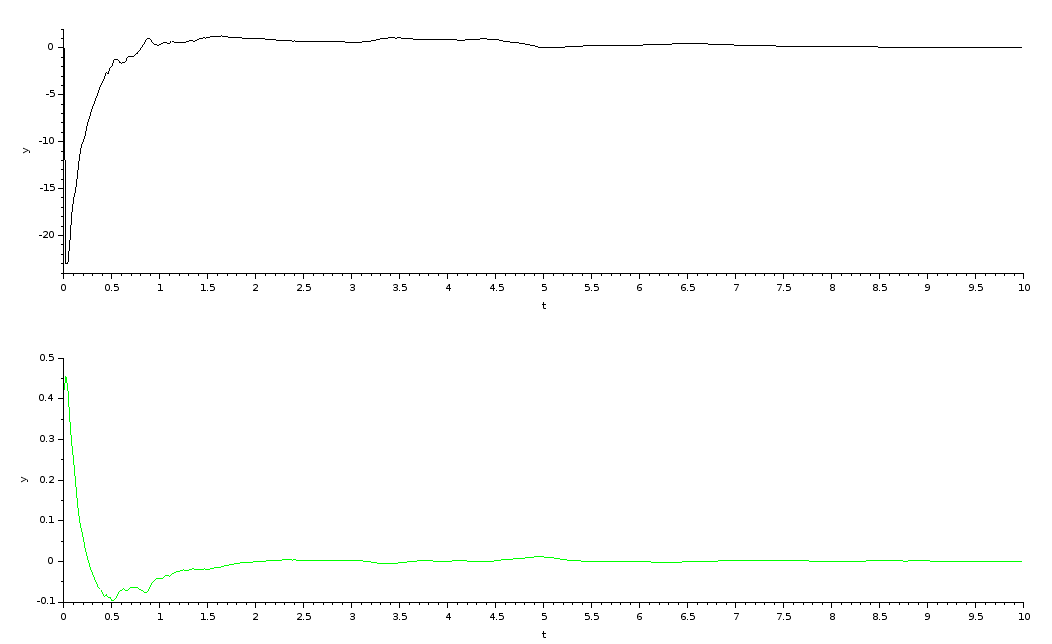
Ábra 3.5-3

Kapocs feszültség-idő

Pozíció-idő

4. Szabalyozo megvalositas

A szakaszról a korábbiakban kiderült, hogy adott szabályozási pontosság (kilengés) mellett egy gyengébb erőforrással rendelkező szabályozó is elláthatja a feladatot. A mindenki asztalán megtalálható PC erre alkalmasnak tűnik némi megkötéssel. Nem lesz valós idejű, de ha nem sűrű és nagy a dTs (jitter), akkor a robosztus szabályozó kezelni tudja a problémát.

Olyan szabalyozot szeretnek tervezni, amely ‘free numerical-computing-programmal’ (Scilab, Octave, Python) van lekezelve es az aktualas / erzekeles van csak implemntalva beagyazott rendszerben.

Lehetosegek

A rendszer megvalósítására különböző opensource / kereskedelmi lehetőségek vannak, az elvárásoktól függően. A könyv céljának megfelelően a nyílt forráskódú rendszerekkel dolgozok.

Az alábbi táblázat a tipikus paramétereket foglalja össze.

Kép - Rendszerek összehasonlítása

RTAI: https://www.rtai.org/?About_RTAI-Lab

X2C: https://x2c.lcm.at/screenshots/

Scilab serial + uC: https://atoms.scilab.org/toolboxes/wgserialxcosio/16.04.1

uC1: https://www.arduino.cc/

uC2: https://www.ti.com/tool/LAUNCHXL-F28379D

PLECS: https://www.plexim.com/products/rt_box

Matlab Speedgoat: https://www.speedgoat.com/products-services/real-time-target-machines/performance

Matlab DSPACE: https://www.dspace.com/en/pub/home/products/hw/simulator_hardware/scalexio/scalexio_labbox.cfm#176_29839

BIOE: http://bioe.sourceforge.net/

Soc:

Raspberry Pi: https://www.raspberrypi.com/

Beagle Bone: https://beagleboard.org/bone

A RaspberryPi-Zero2w, Linux-Debian környezet alkalmasnak tűnt a feladat megvalósítására, ahol egy mag van a szabályozó részére lefoglalva. A Raspberry-n Octave szkript-en  fut a szabályozó algoritmus, amiben az UART kommunikációhoz az “instrument-control” csomag [7] megfelelő. 

A BALLUFF távolság érzékelőt és a motor hajtás invertert egy Arduino Nano kezeli, ami az UART-tx interfészen ütemezi a szabályozót, majd az UART-rx vonalon várja a szabályozó választ, amit az inverter-nek továbbít duty cycle, kapocsfeszültség formájában. Az Arduino elvégzi a hat lépéses motor kommutációt a kapott HALL szenzorok jelei alapján.

A Raspberry Zero2w rendelkezik wifi interfésszel, tehát SSH programmal csatlakozhatunk az eszközhöz, aminek segítségével könnyen elérhetővé válik például az Octave install, git repository, html szerver, GCC cross compile az Arduino CLI [8], tehát a teljes fejlesztő környezet díjmentes, open-source és kis erőforrásigényű, konzolból elérhető. Természetesen a Raspberry lecserélhető egy megfelelően erős asztali számítógépre is.

A rendszer tovább fejleszthető a realtime Linux [13] irányába is, az igényektől függően. Komolyabb real time igények esetén, mint például állandó mágnesű szinkron motor mezőorientált nyomaték szabályozása, a mikrokontrolleres környezet célravezetőbb a perifériák gyors kezelése érdekében.

—-o—-

Kontroller - Scilab, Octave, Python

Problema

A Scilab,Xcos + PC, grafikus window jol mukodik, viszont a ‘Scilab-cli’ sem fut ARM architekturan (PC-n rendben mukodott), mert a TCL-t PC-re szánták. → Octave hasznalata.

A Python control lib + Arduino lib tetszik, de emlekeim szerint nem volt egyszeru a fuggosegek kielegitese telepiteskor, masreszt Ts>50ms-et sikerult UART kommuikacioban elerni, nem valasztottam, de jo irany lehet.

Scilab → XCOS based Solution

Garfikus window feluleten, szkopok hasznataval remekul lathatoak a belso valtozok es aktuator motor feszultseg jel.

Szimulacio, xcos, teljes visszacsatolással

>./ballonwheel/scilab/bow_simulation/BoW_230819_discr20ms.sce

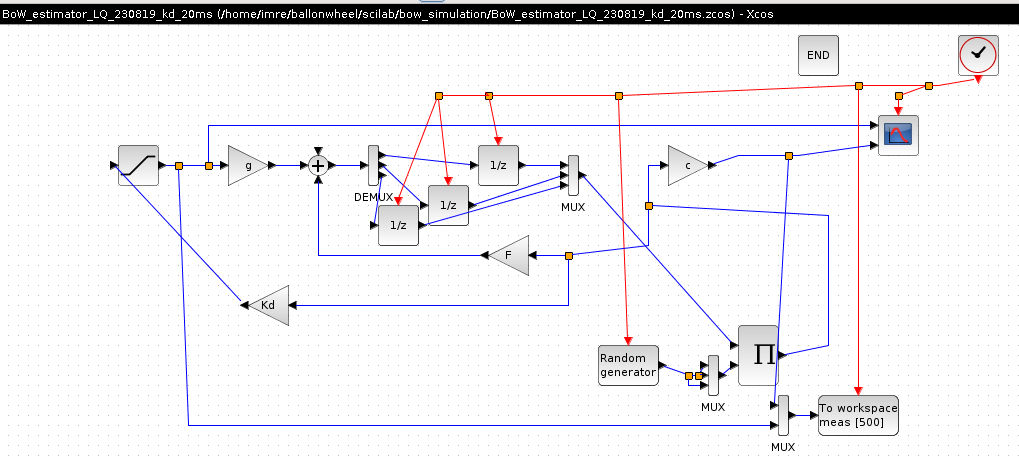
Az x(3) initial erteke 0.4[rad].

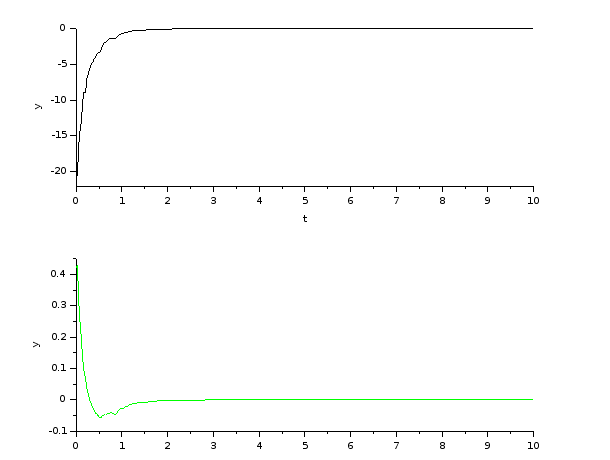
Kepx - teljes vcs, felul motor fesz(u[V]), alul pozicio(x[rad])

Szimulacio, xcos, becslővel

>./ballonwheel/scilab/bow_simulation/BoW_230819_discr20ms.sce

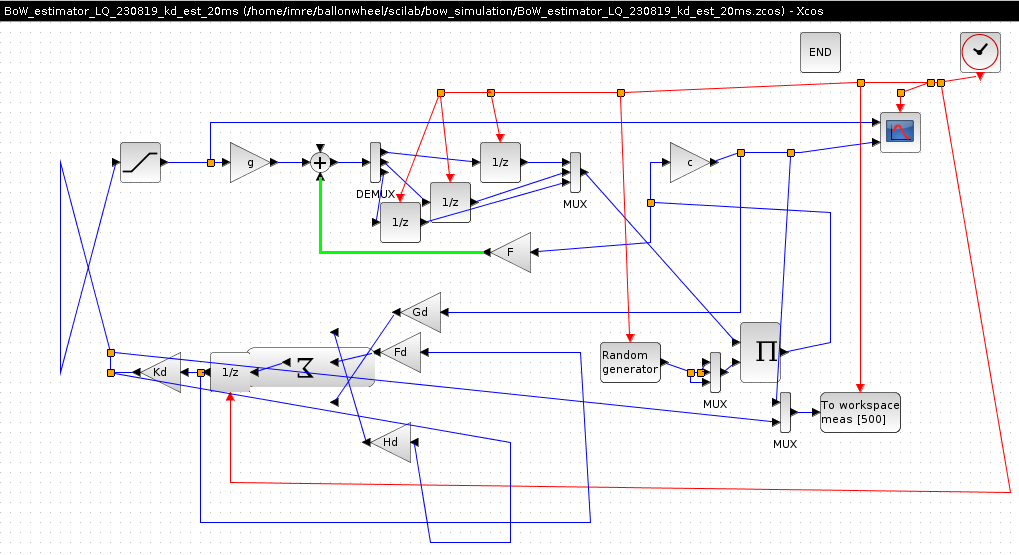
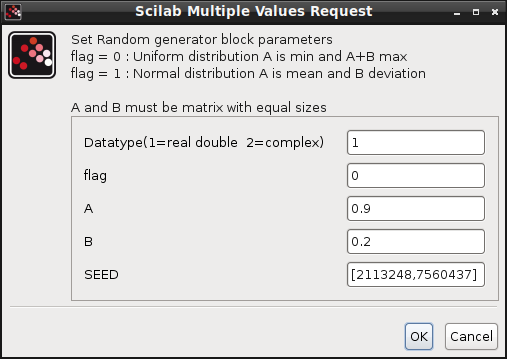
Adatsor generalasa xcos-bol, mert meas.values es maes.time az xcos modellben le lett generalva:

>csvWrite(meas.values, “/home/imre/ballonwheel/scilab/bow_simulation/meas1.values”)

>csvWrite(meas.time, “/home/imre/ballonwheel/scilab/bow_simulation/meas1.time”)

Gondolatkiserlet → sample time csokkentese → min Ts = 150msec

Itt arrol van szo, hogy meddig lehet csokkenteni a Ts-t, hogy meg valami ertelmeset csinaljon a rendszer?

Itt azt tudjuk megvizsgalni, hogy a szakasz milyen minimum beavatkozasi idot kepes elviselni.

Vegyuk eszre, hogy a kulonbozo Ts -hez pl. kulonbozo Fd matrix tartozik!

Ts=20msec

--> Fd

Fd =

0.3234495 0.0000853 -0.0000183

-0.2148639 1.0021797 -0.2185513

-0.0025432 0.0200145 -0.0024805

-o-

Ts=150msec

--> Fd

Fd =

-0.0000275 0.0014552 -0.0021628

-0.3482255 1.1239824 -1.6808812

-0.0433773 0.156157 -0.2322016

Itt mar oszcillalva all be, tovabb novelve Ts = 200msec eseten mar nem kepes beallni.

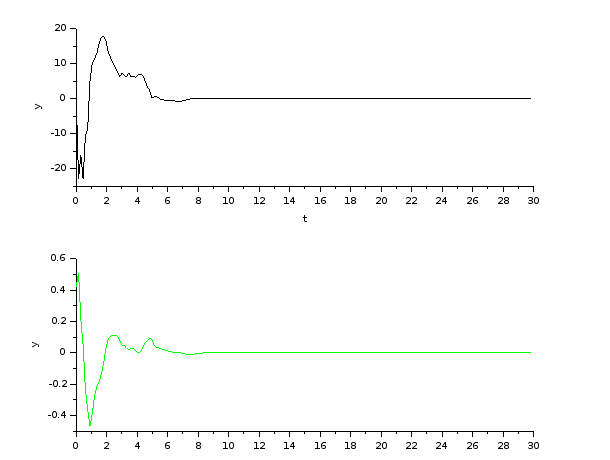
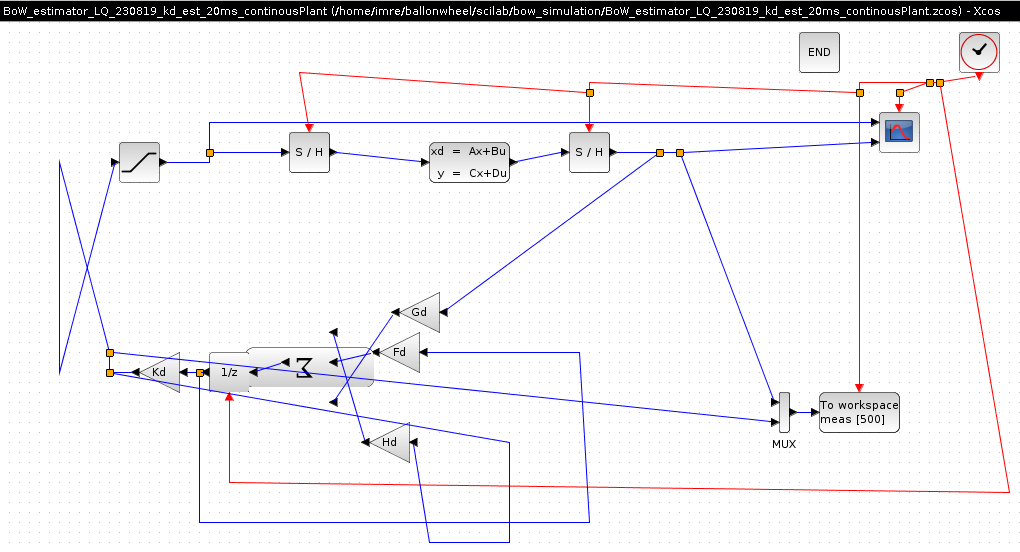
Kepx, diszkret szakasz es kontroller modell becslovel, Ts=150msec, oszcillalva all be

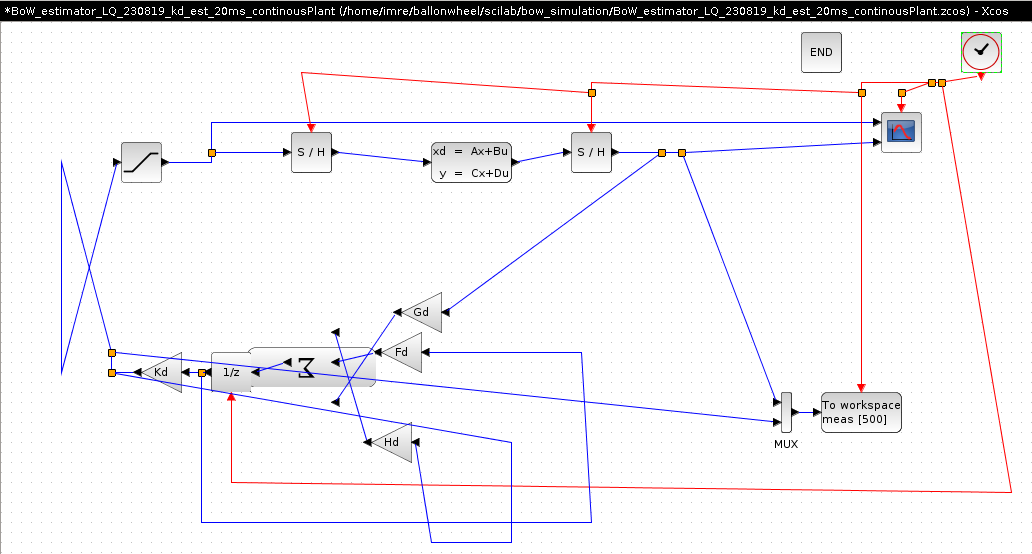
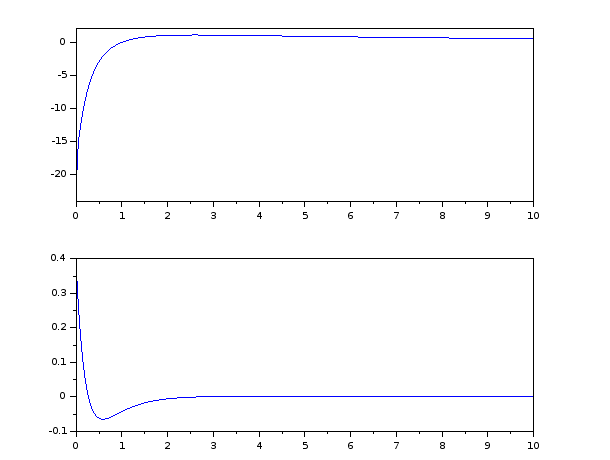
Kepx, folyamatos ideju szakasz model es diszkret kontroller becslovel

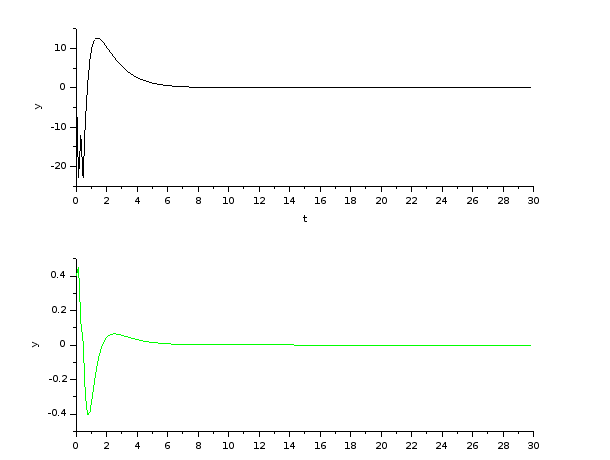
Kepx, folyamatos ideju szakasz modell es diszkret kontroller becslovel, Ts = 150msec

Gondolatkiserlet → elterni a Ts-tol → labilis lesz

Itt arrol van szo, hogy a diszkret idobe valo attereskor (ABCD → gFcd) megadott Ts-tol eltero Ts-sel hivogatjuk a kontroller algoritmust, akkor mi tortenik?

Ts - ezzel az idovel lett kiszamolva a diszkret plant: BoW_ssd=dscr(BoW_ss, 0.02), //20msec

Tcall - ezzel az idovel hivogatjuk a kontrollert → szimulacioban az “ora”.

Kovetkeztetes: A Tcall viszonylag kis novelesevel, mar hamar labilis lesz a rendszer.

Fontos, hogy a szakasz folyamatos idoben van szamolva es a hozza tartozo becslo diszkretizacio Ts=20msec helyett Tcall=30msec eseten mar oszcillal a rendszer.

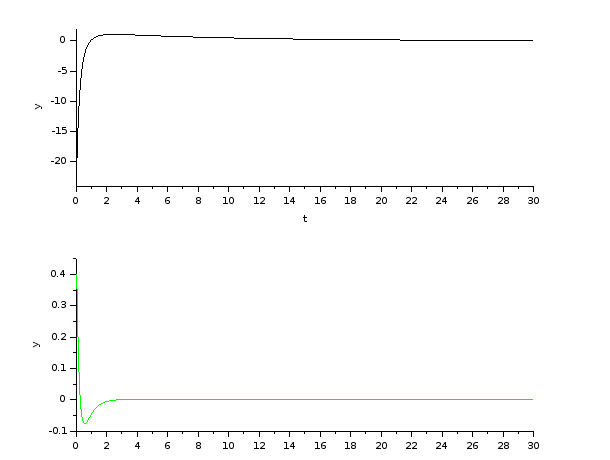
Kepx- becslovel, Ts=20msec, Tcall=20msec → Tsettle=2sec

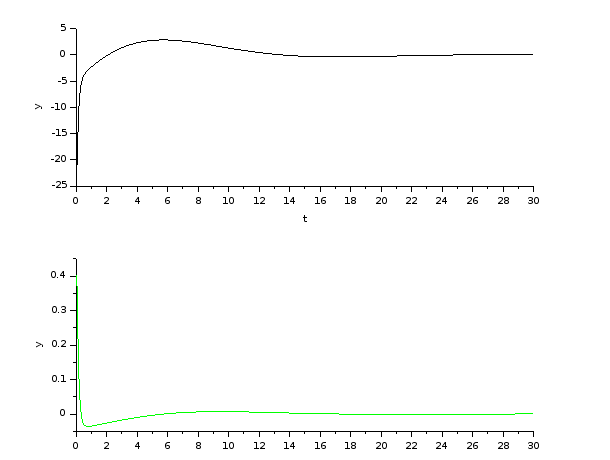
Kepx- becslovel, Ts=20msec, Tcall=30msec → Tsettle=oszcillal

Szimulacio, script, teljes vcs

‘./ballonwheel/scilab/bow_simulation/plantFeedback_discrete.sce’

x = [0;//ww

0;//w2

0.4];//fi2

u = 0;

sum_zn1=[0;0;0];

i=0;

while i<500

i=i+1;

if((x(3)<%pi/2) && (x(3)>-%pi/2))then //vegallas

disp(i)

//controller

u=Kd*x;//<-------------------------------------------------teljes vcs

//estimator

//sum_zn1=Fd*sum_zn1+Gd*x(3)+Hd*u;

//u=Kd*sum_zn1;

if(u>24)then

u=24;

end

if(u<-24)then

u=-24;

end

disp("u")

disp(u)

meas.values(i,1)=u;

//plant

xp=F*x+g*u;

x=xp;

disp("x")

disp(x)

meas.values(i,2)=x(3);

meas.time(i)=(i-1)*0.02;

//y=C*x+D*u;

//disp("y")

//disp(y)

end

end

subplot(2,1,1)

plot(meas.time, meas.values(:,1))

subplot(2,1,2)

plot(meas.time, meas.values(:,2))

csvWrite(meas.values, '/home/imre/ballonwheel/scilab/bow_simulation/meas2_values.csv')

csvWrite(meas.time, '/home/imre/ballonwheel/scilab/bow_simulation/meas2_time.csv')

Szimulacio, script, becslo

‘./ballonwheel/scilab/bow_simulation/plantFeedback_discrete.sce’

-o-

//sof

x = [0;//ww

0;//w2

0.4];//fi2

u = 0;

sum_zn1=[0;0;0];

i=0;

while i<500

i=i+1;

if((x(3)<%pi/2) && (x(3)>-%pi/2))then //vegallas

disp(i)

//controller

//u=Kd*x;

//estimator

sum_zn1=Fd*sum_zn1+Gd*x(3)+Hd*u;

u=Kd*sum_zn1;

if(u>24)then

u=24;

end

if(u<-24)then

u=-24;

end

disp("u")

disp(u)

meas.values(i,1)=u;

//plant

xp=F*x+g*u;

x=xp;

disp("x")

disp(x)

meas.values(i,2)=x(3);

meas.time(i)=(i-1)*0.02;

//y=C*x+D*u;

//disp("y")

//disp(y)

end

end

subplot(2,1,1)

plot(meas.time, meas.values(:,1))

subplot(2,1,2)

plot(meas.time, meas.values(:,2))

csvWrite(meas.values, '/home/imre/ballonwheel/scilab/bow_simulation/meas3_values.csv')

csvWrite(meas.time, '/home/imre/ballonwheel/scilab/bow_simulation/meas3_time.csv')

//eof

-o-

Valos setup

Linux, Scilab script, XCOS, WGSerial - ArduinoNano, BTS_Inverter

WGserial + 6step + tavolsag erzekelo merge

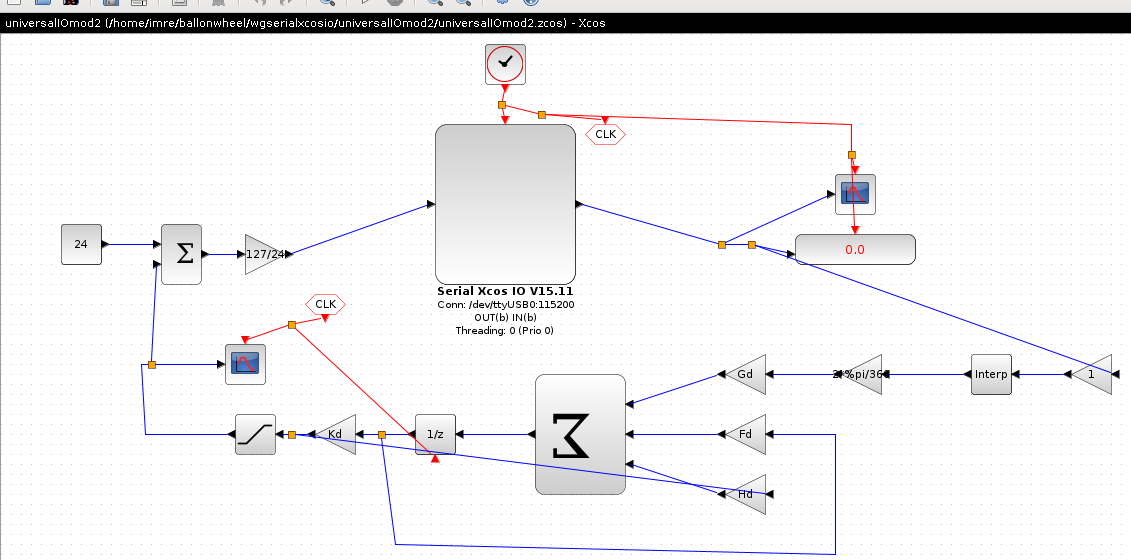
Ahhoz, hogy a modellbol elerheto legyen a motor es a tavolsag erzekelo egyesiteni kellett a motor hajtast, a tavolsag erzekelo ADC-t es a WGserail kodot.

Scilab valos setup vegeredmeny

https://drive.google.com/file/d/11ZUFCLI1WgMBgq3CjRYAuPaKNTTK7fin/view?usp=drive_link

Octave → BASH based Solution

A cel az, hogy a linux startup utan automatikusan induljon a kontroller- Ezt scilab-cli-vel nem sikerult elernem (arm-on), lasd korabban. Octave alkalmasnak tunik.

Az inicializacios szkript atirasat lasd a mellekletben, ami a fullrf() fv-t kiveve siman ment.

Kontroller - simulation, script

x = [0;#ww

0;#w2

0.4];#fi2

u = 0;

sum_zn1=[0;0;0];

i=0;

while i<500

i=i+1;

disp(i)

#controller

#u=Kd*x;

#controller+estimator

sum_zn1=Fd*sum_zn1+Gd*x(3)+Hd*u;

u=Kd*sum_zn1;

if(u>24)

u=24;

end

if(u<-24)

u=-24;

end

disp("u")

disp(u)

xp=F*x+g*u;

x=xp;

disp("x")

disp(x)

#y=C*x+D*u;

#disp("y")

#disp(y)

meas.values(i,1)=x(3);

meas.values(i,2)=u;

meas.time(i,1)=(i-1)*0.02;

endwhile

subplot(2,1,1)

plot(meas.time, meas.values(1:end,1),'g');

hold on;

subplot(2,1,2)

plot(meas.time, meas.values(1:end,2),'b');

pause(10)

#measAll=[meas.time meas.values];

csvwrite('./meas4_values.csv',meas.values)

csvwrite('./meas4_time.csv',meas.time)

#csvwrite('./mAll.csv',measAll)

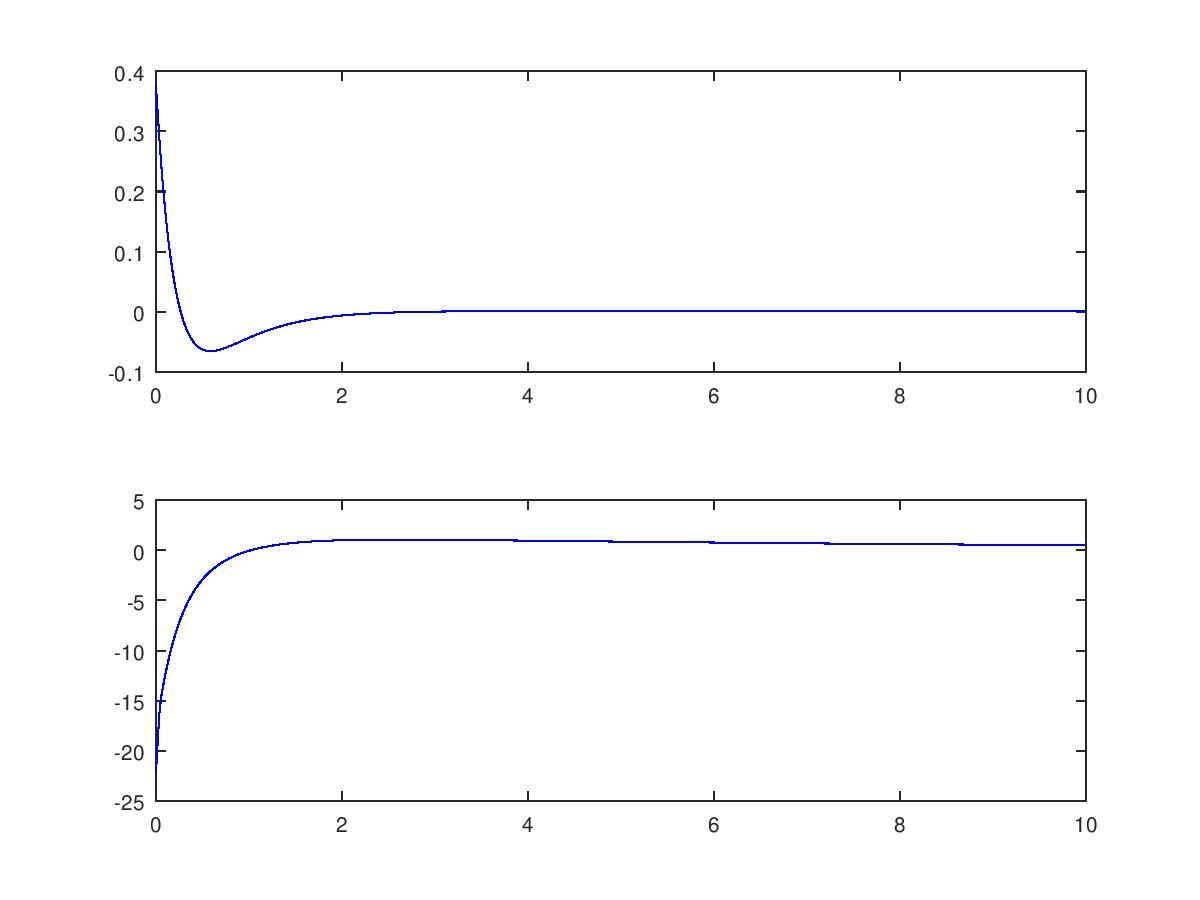
-o-

gnuplot

set terminal dumb

plot sin(x)

https://raymii.org/s/tutorials/GNUplot_tips_for_nice_looking_charts_from_a_CSV_file.html

gnuplot> set terminal dumb

gnuplot> set datafile separator ','

gnuplot> plot "C:/Users/dio2bp/Desktop/tmp/bow/mAll.csv" using 2 with lines

gnuplot> plot "C:/Users/dio2bp/Desktop/tmp/bow/mAll.csv" using 3 with lines

Osszehasonlitas Scilab szkript eredmenyekkel

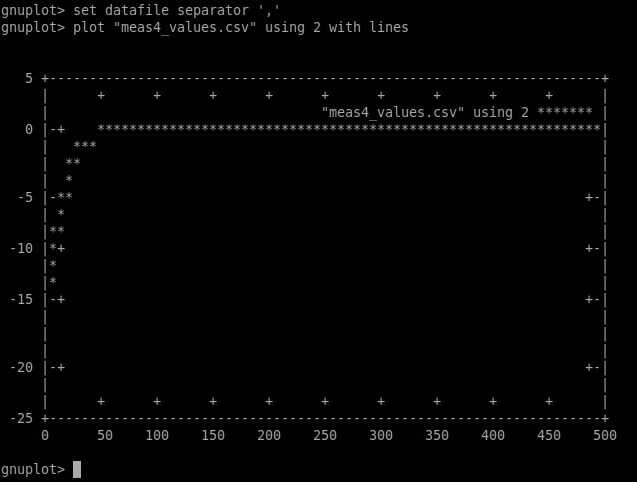
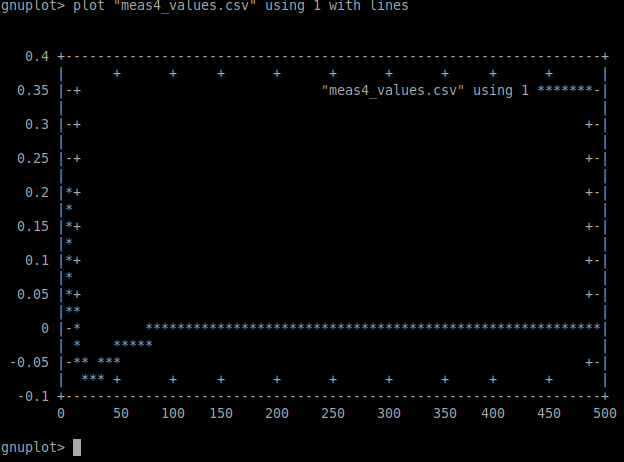
Plot csv-bol

• meas1: Scilab xcos

• meas2: Scilab szkript teljes vcs

• meas3: Scllab szkript becslo

• meas4: Octave szkript becslo

meas1_time=csvRead('/home/imre/ballonwheel/scilab/bow_simulation/meas1_time.csv')

meas1_values=csvRead('/home/imre/ballonwheel/scilab/bow_simulation/meas1_values.csv')

meas2_values=csvRead('/home/imre/ballonwheel/scilab/bow_simulation/meas2_values.csv')

meas3_values=csvRead('/home/imre/ballonwheel/scilab/bow_simulation/meas3_values.csv')

meas4_values=csvRead('/home/imre/ballonwheel/scilab/bow_simulation/meas4_values.csv')

subplot(2,1,1)

plot(meas1_time, meas1_values(:,1))

plot(meas1_time, meas2_values(:,2))

plot(meas1_time, meas3_values(:,2))

plot(meas1_time, meas4_values(:,1))

subplot(2,1,2)

plot(meas1_time, meas1_values(:,2))

plot(meas1_time, meas2_values(:,1))

plot(meas1_time, meas3_values(:,1))

plot(meas1_time, meas4_values(:,2))

Scheduler loop

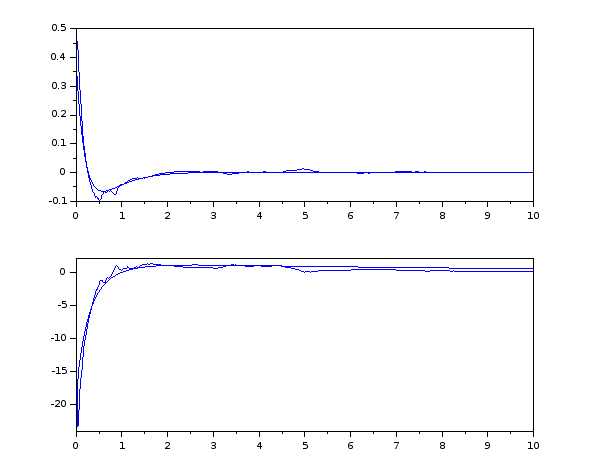
Korabban a Scilab Xcos megoldasnal a modellben az idozito megoldotta a 20msec-es loop-ot es a WGserial library megoldotta a kommunikaciot.

Itt a szkriptes megoldasnal

• Linux:

  • Octave loop,

  • instrument-control package: fread(), fwrite()

• Arduino:

  • Uart kommunikacio,

  • 6step hajtassal integralni,

  • tavolsag mero ADC-vel integralni

  • Scheduler - ADC utem - Ts=20msec-100msec

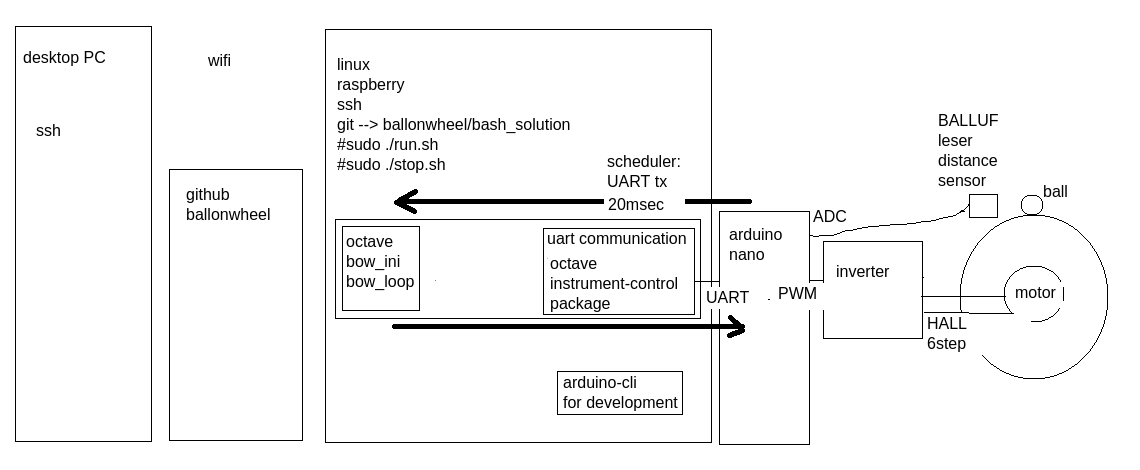
Kepx, teljes rendszer osszallitas

Ahogy az erzekelonel irtam, az ADC interrupt-jahoz igazodik a rendszer uteme, tehat ez a sampling time, Ts. Az arduinoNano-ADC egyszeruen csak kikuldi az 3 byte-os keretet es varja a 3 bajtos keretet valaszul.. A fentiekbol kovetkezik, hogy linux-on futo rendszernek a Ts ido alatt ki kell szolgalnia a kommunikaciot es a kontroller szamolast.

Tapasztalat alapjan 5msec-ig le lehet menni (rPiZero2w, 1Ghz, 4 core, 512M) 10ppm hibaval sajat C kod alapjan, mig octave-intrument-control package-val ez 20msec.

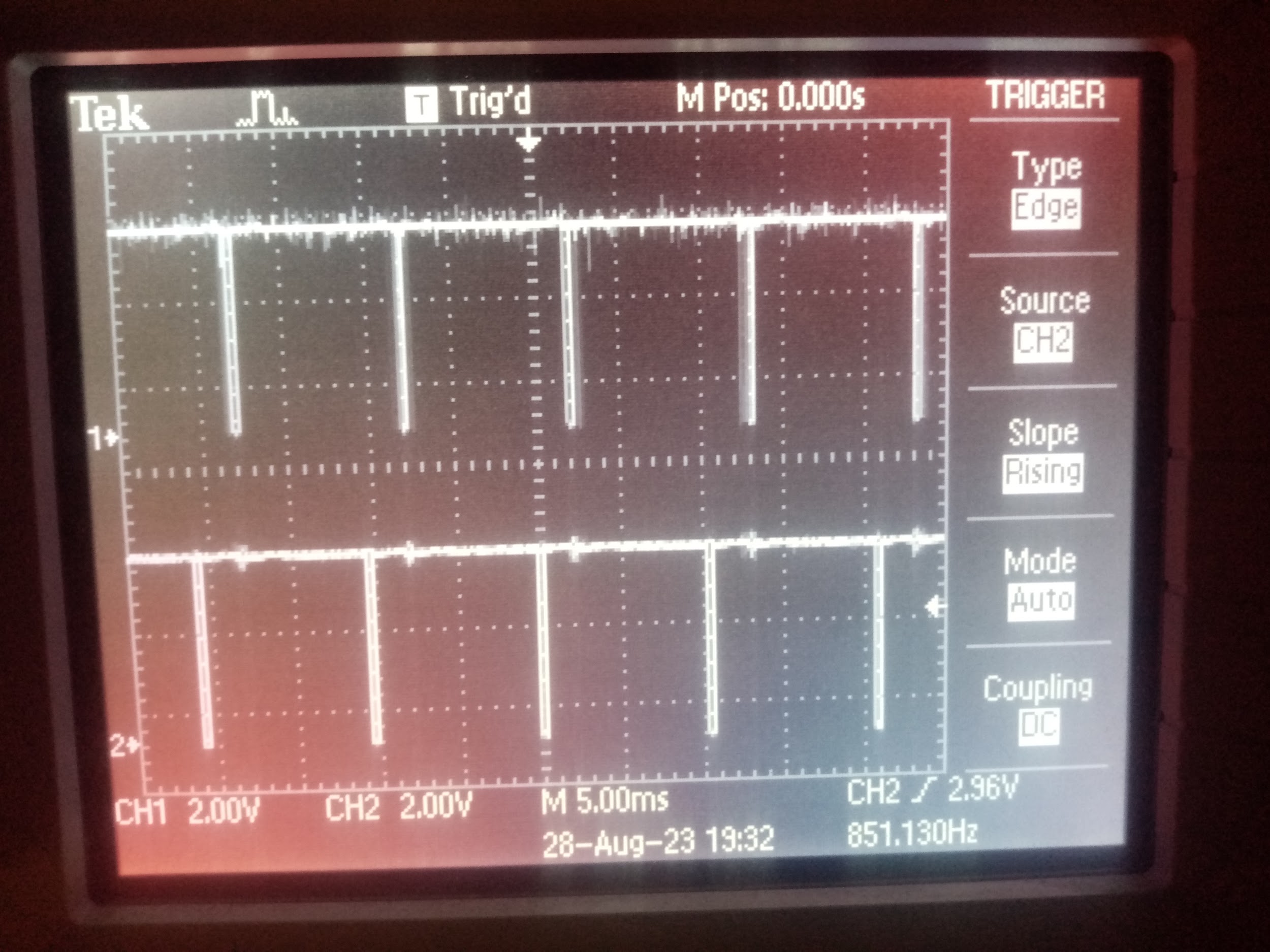
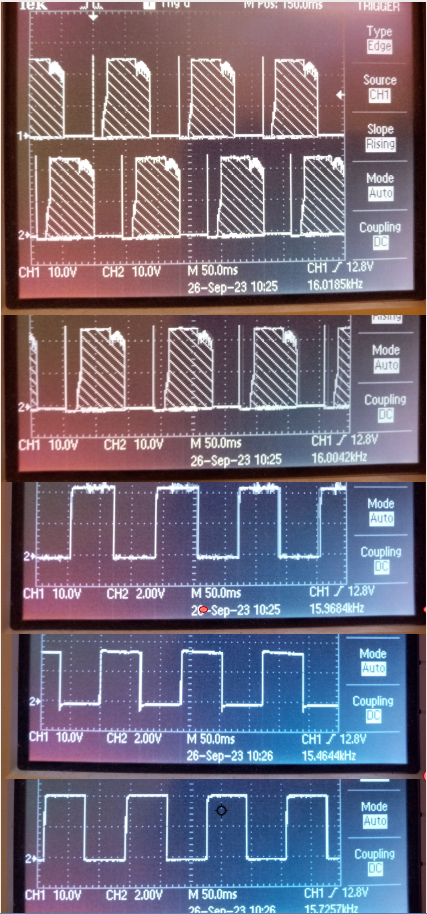
Arduino, CH1:rx CH2:tx

Softrealtime

Habar a PC, SoC - Linux megoldas egyszeruve teszi a kontroller megvalositast, de nem egyszeru vele elerni a real time-ot (RTAI). Kozelito megoldasnak a soft real time Linux jo lehetoseg.

1, RT Linux: PC-re Debian alatt “apt-get install linux-image-rt-amd64” paranccsal konnyen elerhet, de ARM-ra kulon kernel-t kell forditani.

2, Tovabbi lehetoseg a core-ok hasznalatanak meghatarozasa a processzek szamara, lasd a kovetkezo fejezetben.

3, prioritas beallitasa: >nice –20 octave script.m

Raspberry RT kernel & Core Selection

http://comfilewiki.co.kr/en/doku.php?id=comfilepi:improving_real-time_performance:index

sudo apt install cpufrequtils

sudo cpufreq-set -g performance

sudo cat /sys/devices/system/cpu/cpu[0-3]/cpufreq/cpuinfo_cur_freq

vcgencmd measure_clock arm

First, add isolcpus=nohz,domain,managed_irq,3 irqaffinity=0-2 nohz_full=3 rcu_nocbs=3 to the /boot/cmdline.txt file. This will prevent Linux from allocating the 4th core to most process, interrupt handlers, and kernel threads. Reboot for the change to take effect.

Get the PID - bash-bol majd

sudo taskset -cp 3 1176

sudo chrt -f -p 1 1176`

Na ez utan nem lehet kommunikalni a rasberryvel

Ezt inkabb nem javasoljak, hanem ,legyen sleep, ha meg kell varni:

sudo sh -c "echo -1 > /proc/sys/kernel/sched_rt_runtime_us"

UART kommunikacio

Problema

1, Scilab szkript nem megy az uart lib, mert TLC csak grafikusban megy - octave kell

2, Jo lett volna megoldani bash-bol az UART kommunikaciot az egyszeruseg kedveert.

Habar mukodik a dolog, de nem robosztus (uart_rxtx.sh), marad a C code (main.c).

Az is nagy tapasztalat, hogy egy processzben nem lehet megoldani az uart kuldest-fogadast, tehat egyszerubb volt az arduino oldalrol utemezni es kiszolgalni a kovetkezo beerkezo adatig. Ily modon az arduino oldal a master.

3, uart C code, ezzel el lehet erni az 5msec rx-tx loop-ot

4, octave instrumant-control tool: ez 20msec loop lehet (raspZero2w) → ez lett.

Szkriptek, run.sh, stop.sh

./ballonwheel/bash_solution

./run.sh

• Cpu orajel legyen pontosabb

• (Magok kivalasztasa, meg nem hasznalom, tesztelni kell)

• Startup.sh

  • Ki kene talalni hol van az arduino ttySB0,1,2…

  • Chmod 777

  • Setseial lowlatency, de ez csak eredeti FTDInal megy, de a kinaival is megy a 20 msec

• Octave prioritas magasra allit

• Octave ini es loop start

• Kommunikacio start

• Megjegyezni a processz IDket

./stop.sh

• Kill octave

./help.sh

• Egy aprocska manual

Kontroller - valos setup

Most hogy a modell szimulacioban fut Octave szkriptben atterhetek a valos setup-ra:

• 6 step motor hajtas integralas

• ADC erzekelo integralas

• kalibralas

• Octave loop.

  • Adc → bow_position→ szogelfordulas

  • U → scale→ bow_motor

• Gnuplot realtime

  • https://stackoverflow.com/questions/44470965/how-can-you-watch-gnuplot-realtime-data-plots-as-a-live-graph-with-automatic-up

https://octave.sourceforge.io/arduino/package_doc/Protocol-based-I_002fO-Overview.html

https://wiki.octave.org/Arduino_package

https://docs.octave.org/latest/

https://techfun.sk/hu/produkt/vykonny-motor-driver-43a-h-bridge-bts7960/?lang=hu&currency=HUF&gclid=CjwKCAjw5MOlBhBTEiwAAJ8e1lFYeX2Sl_gbaAqPTRCA_KZHF_Bmf9QzmBEOzAYtyjg6osGrWSYHdBoCWq8QAvD_BwE

Octave Script Setup, Eredmeny

https://drive.google.com/file/d/1QCgao47FQXtr-xK46_ASLiKJgwR6ucpj/view?usp=drive_link

Python, proba, nem hasznalt

Python control system + uart

https://python-control.org

https://python-control.readthedocs.io/en/0.9.4/intro.html

https://www.xanthium.in/linux-serial-port-programming-using-python-pyserial-and-arduino-avr-pic-microcontroller

Python DSP

https://docs.scipy.org/doc/scipy/reference/signal.html

https://www.electronicwings.com/raspberry-pi/raspberry-pi-uart-communication-using-python-and-c

https://pyserial.readthedocs.io/en/latest/index.html

https://www.hackster.io/vincekok/part-2-uart-serial-communication-python-arduino-0476eb

sudo apt install python3-pip

pip install pyserial

https://problemsolvingwithpython.com/11-Python-and-External-Hardware/11.03-Controlling-an-LED/

ser = serial.Serial('COM4', 9800, timeout=1)

time.sleep(2)

user_input = 'L'

while user_input != 'q':

user_input = input('H = on, L = off, q = quit' : )

byte_command = encode(user_input)

ser.writelines(byte_command) # send a byte

time.sleep(0.5) # wait 0.5 seconds

print('q entered. Exiting the program')

ser.close()

https://www.odoo.com/forum/help-1/how-to-install-pip-in-python-3-on-ubuntu-18-04-167715

5. Beavatkozó szerv, Motor Hajtás Megvalósítás

A HUB motor(36V/300W) az aktuátor, amit Hall szenzorral six-step hajtással lehet és elegendő hajtani.

HALL szenzor nélkül lehetne BEMF, BLDC hajtast open-loop inditassal.

Az FOC hajtást szenzorral vagy open-loop indítással pozíció becslovel lehetne hajtani, kisebb nyomatek hullamossaggal, de a jelen problemaban az indito nyomatekra van szukseg, amit legjobban HALL szenzor, six-steppel lehet legjobban elerni. Erdekes megoldas lehetne FOC hajtas a HALL jelek kozti interpolacioval, de erre nincs szukseg.

/******************************

43 6 step drive

44 built from scretch

45 1, choose phases of A, B, C as you want but later insist on

46 A-PH yellow

47 B-PH green

48 C-PH blue

49 A-HALL yellow

50 B-HALL green

51 C-HALL blue

52

53 2, define the cw and ccw direction and insist on

54 definition: torque vector as a right hand rule, so that

55 ha a nyomatek vektor pozitiv es felem nez, akkor az irany: ccw

56 Tehat mot a nyomatek legyen pozitiv a faziskabel bekotesi oldala felol nezve.

57

58

59 3, measure BEMF, A-B, B-C, C-A

60

61

62 4, measure HALL relative to BEMF

63 HALLs are 120degree from each other.

64 HALLs are high at its respective phase is positive half periode 180 degree.

65 Ex.:

66 phase +A-C --> A-HALL

67 phase +A-C --> B-HALL

68 phase +A-C --> C-HALL

69

70 *

71 * * *

72 * * *

73 * *

74 *

******* ****

76 * * *

77 * *******

78

79 4, check and make sure of the microcontroller HALL input order ex.

80 d5 D5 2^0 A-HALL

81 d6 D6 2^1 B-HALL

82 d7 D7 2^2 C-HALL

83

84 5, put vectors on motor and check the HALL signals

85 [BH_CL] // 0b001 0x1

86 [BH_AL] // 0b011 0x3

87 [CH_AL] // 0b010 0x2

88 [CH_BL] // 0b110 0x6

89 [AH_CL] // 0b101 0x5

90 [AH_BL] // 0b100 0x4

91

92 6, rotate, ex. manually cw and check the HALL step order, ex.

93 5 1 3 2 6 4

94

95 7, creat the commutation table of cw

96 in case 5[AH_BL] -> call 1[AH_CL],

97 in case 1[AH_BL] -> call 3[AH_CL],

98 in case 3[AH_BL] -> call 2[AH_CL],

99 in case 2[AH_BL] -> call 6[AH_CL],

100 in case 6[AH_BL] -> call 4[AH_CL],

101 in case 4[AH_BL] -> call 5[AH_CL],

102

103

104 8, rotate ccw

105 4 6 2 3 1 5

107 9, create the commutation table of ccw

108 call next vector according to direction

109 in case 4[AH_BL] -> call 6[CH_BL],

110 in case 6[CH_BL] -> call 2[CH_AL],

111 in case 2[CH_AL] -> call 3[BH_AL],

112 in case 3[BH_AL] -> call 1[BH_CL],

113 in case 1[BH_CL] -> call 5[AH_CL],

114 in case 5[AH_CL] -> call 4[AH_BL],

115

116

117 9, creat the commutation table of cw

118 in case 4[AH_BL] -> call 6[AH_CL],

119 in case 4[AH_BL] -> call 6[AH_CL],

120 in case 4[AH_BL] -> call 6[AH_CL],

121 in case 4[AH_BL] -> call 6[AH_CL],

122 in case 4[AH_BL] -> call 6[AH_CL],

123 in case 4[AH_BL] -> call 6[AH_CL],

124

125 10, some alignment is necessary whether HALL is properly placed or not relative to stator coils.

[main e44b08b] marad az elozo verzio, mert: arduinov3.ino_ 1, forditva van, mint a konvencio: ccw-4 2 6 3 1 5, ezert cserelni kene, cw-ccw 2, jelenleg forditva vannak ertelmezve a vektorok Hih-low tok veletlenul, ezert jo de ha meforditom, akkor elegge morogva lepeget --> 30for eltolassal szetesik valoszinuleg a low side pwn (invert pwm) megforditja a vektorokat

1 file changed, 716 insertions(+)

Inverter schematic

BTS7960-M

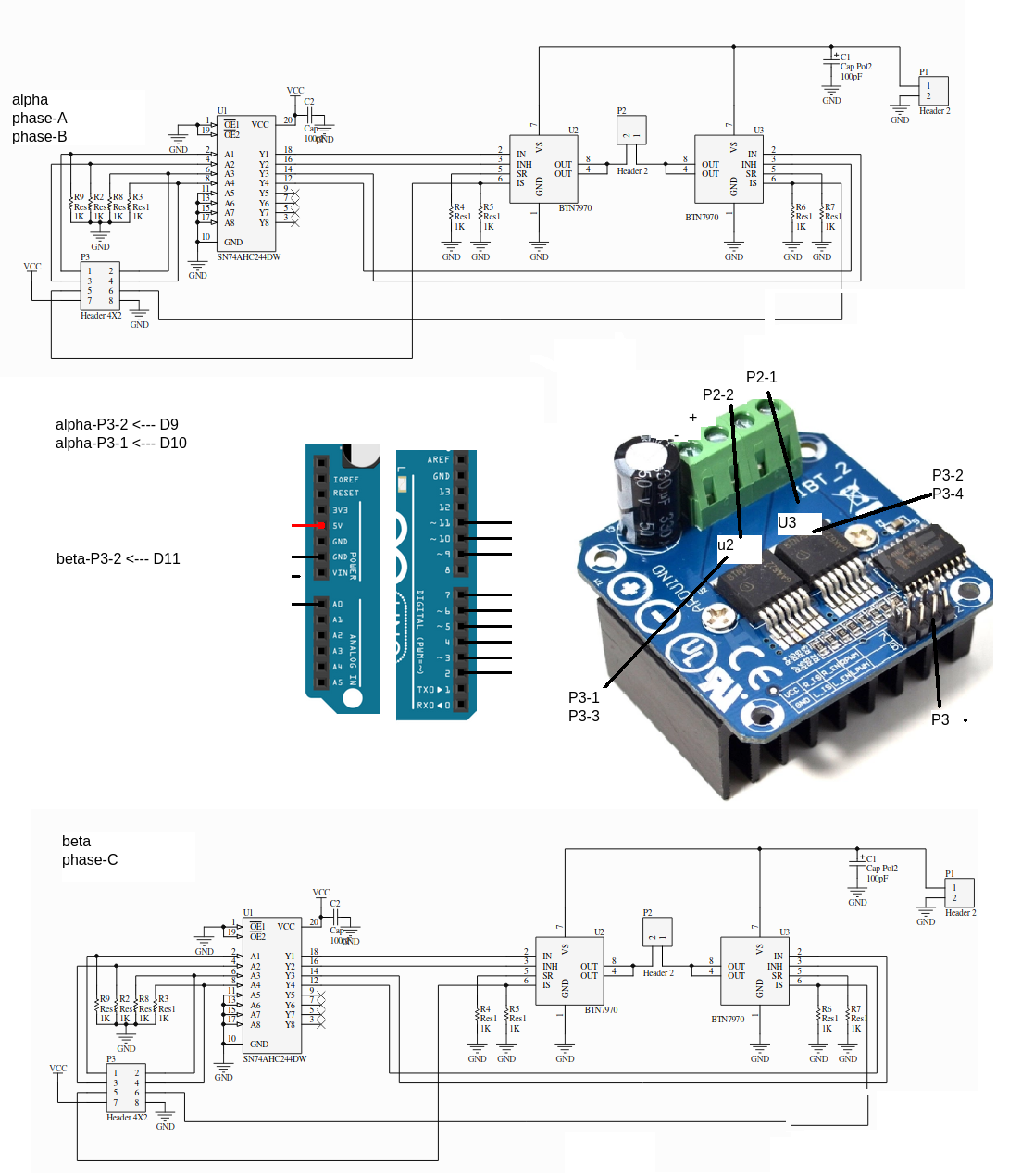
OCR1A = duty; // Set pin 9 PWM duty cycle

OCR1B = duty; // Set pin 10 PWM duty cycle

OCR2A = duty; // Set pin 11 PWM duty cycle

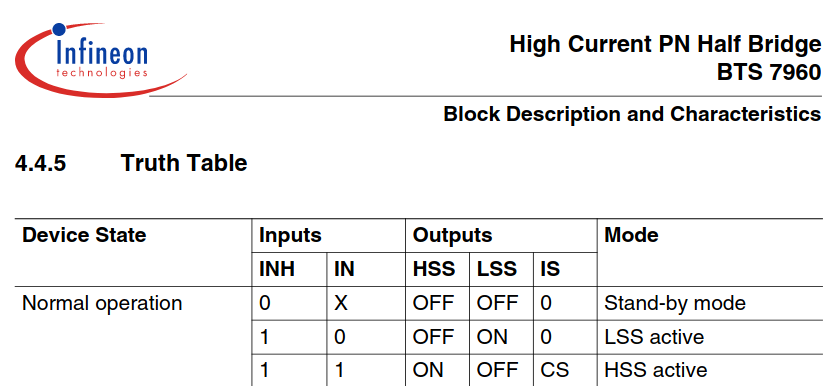
https://ww1.microchip.com/downloads/en/Appnotes/00885a.pdf

https://ww1.microchip.com/downloads/aemDocuments/documents/OTH/ApplicationNotes/ApplicationNotes/SensorlessBLDCAN901a.pdf

https://www.microchip.com/stellent/groups/sitecomm_sg/documents/devicedoc/en543044.pdf

https://www.microchip.com/content/dam/mchp/documents/parked-documents/BLDC%20MC%2000957a.pdf

https://onlinedocs.microchip.com/pr/GUID-0607E6C7-3E40-4169-A33F-0462792573CC-en-US-7/index.html?GUID-A9C9E99B-6C79-47B8-A57C-25636DE6BD8C

https://simple-circuit.com/arduino-cd-rom-brushless-motor-control/

https://simple-circuit.com/arduino-sensorless-bldc-motor-controller-esc/

https://www.microchip.com/content/dam/mchp/documents/parked-documents/BLDC%20MC%2000957a.pdf

https://www.microchip.com/stellent/groups/sitecomm_sg/documents/devicedoc/en543044.pdf

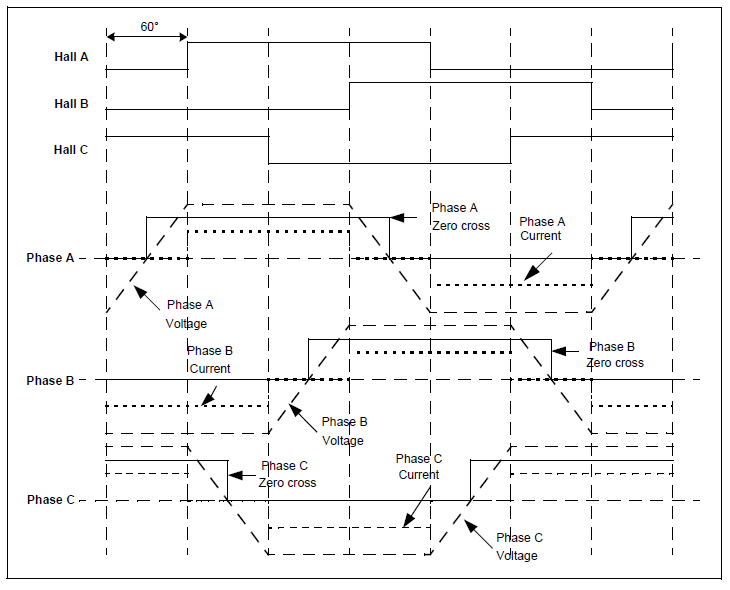
_____________C B A HC HB HA LC LB LA

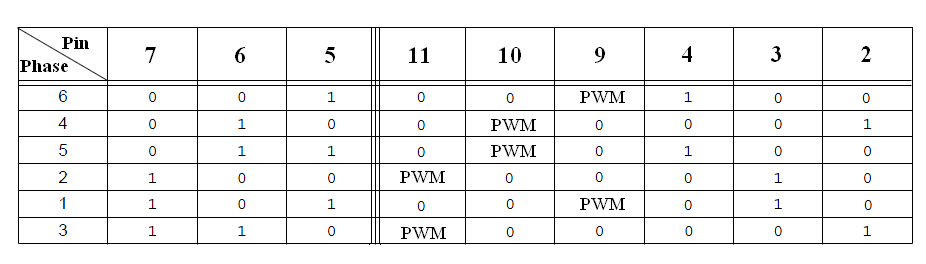
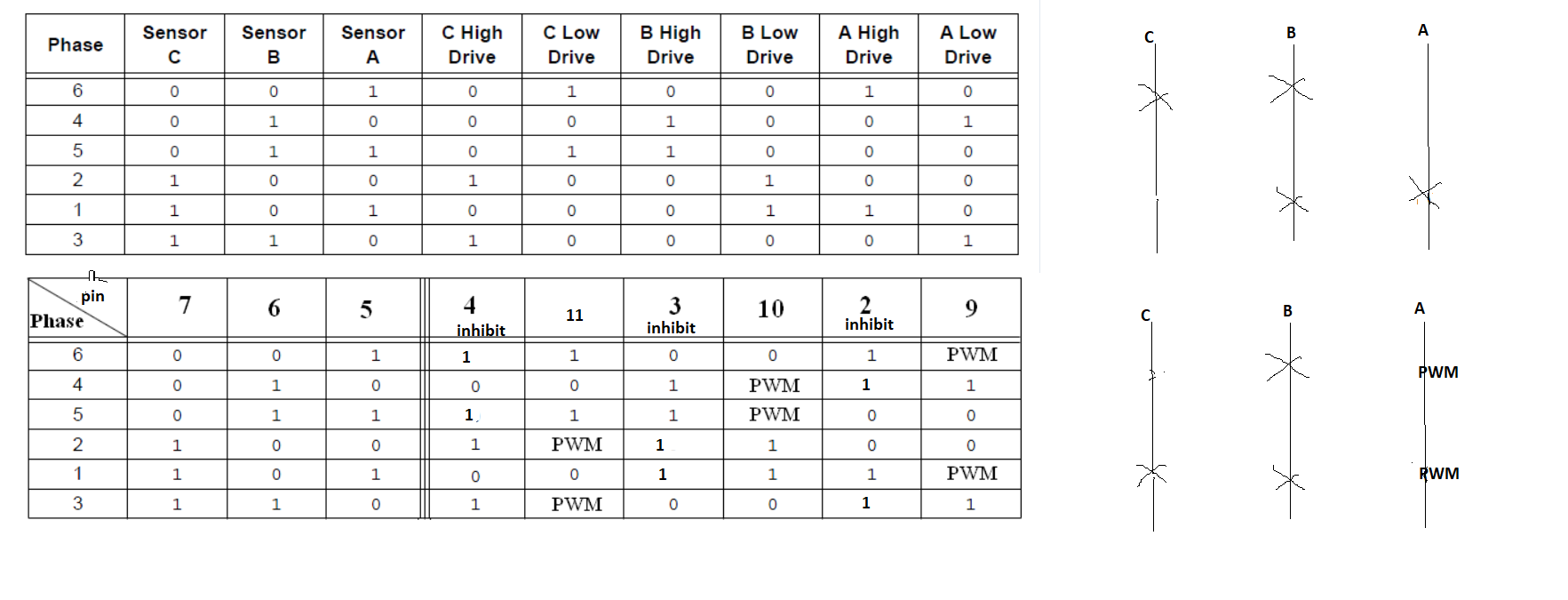
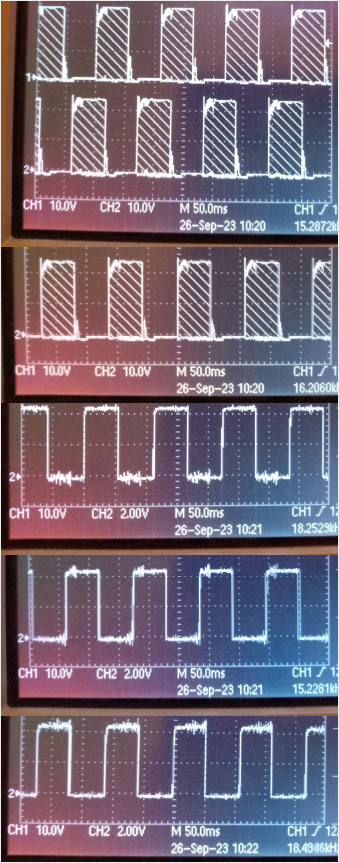
Meres1 CW

Fazis

Sarga → trigg, CH1, tobbi CH2

Zold

Kek

Hall

Sarga

Zold

Kek

if(dir == CW_)

switch(bldc_step){

case 1:

AH_CL();

break;

case 2:

BH_AL();

break;

case 3:

BH_CL();

break;

case 4:

CH_BL();

break;

case 5:

AH_BL();

break;

case 6:

CH_AL();

break;

default:

//PORTD = 0xe0;

break;

Meres2 CCW

Fazis

Sarga → trigg, CH1, tobbi CH2

Zold

Kek

Hall

Sarga

Zold

Kek

case 1:

AL_CH();

break;

case 2:

BL_AH();

break;

case 3:

BL_CH();

break;

case 4:

CL_BH();

break;

case 5:

AL_BH();

break;

case 6:

CL_AH();

break;

default:

//PORTD = 0xe0;

break;

6. Erzekeles, BALLUF → ADC → scheduler

Arduino Nano ADC ch0 - 8bit - 10khz → scheduler → Ts

Szenzor kalibralas

Fesz oszto

Felso tagok 2kohm 3.2kohm

Also tagok 4.7kohm

Vegallasok, vizszintes

11,10V 5,000V 330mm 225adc

5,130V 2,270V 201mm 130adc

0,920V 0,397V 095mm 090adc

posx=[0;24;40;64;100;130;160;190;210;245;255];#[ADC8bit]

posy=[-18.0;-17.0;-15.0;-10.0;-5.0;0.0;5.0;10.0;15.0;17.0;18.0];#[fok]

CONTROLRANGE_DEGREE = 13;

CONTROLRANGE = CONTROLRANGE_DEGREE*2*pi/360;

7. Motor paraméter identifikáció

A szabályozó megvalósítást a motor paraméterek (Ls, Rs, Iw, Km, Ke) meghatározása megelőzte, amely a 1. táblázatban található. A motor szemrevételezése és típusa alapján egy 36V-os 300W-s szinuszmezős állandó mágnesú szinkron HUB hajtás motor (PMSM) kerül alkalmazásra. 

A ‘Ke = U peak / w mech’ értéke a BEMF üresjárási kapocsfeszültségből és a motor ismerete alapján, (46 mágnes, tehát 23 póluspár és 3*17 állórész tekercs) meghatározható. A ‘Km = 3/2 Ke’ a PMSM motoroknál ismert [9]. Az Rs, Ls értékek RLC méréssel kerültek meghatározásra, míg Iw inercia arányossággal történt: ΣM = Iw * βw1 , ΣM = Iw * βw2

Tehát meg kell mérni a kerék fordulatszám felfutási idejét álló helyzetből maximális értékre terhelés nélkül, majd ismert terheléssel. A felfutási idő valamint a terhelő súlyok ismeretében a kerék tehetetlenségi nyomatéka jó közelítéssel meghatározható. A terhelő súlyokat a kerék peremén a lehető legjobban elosztva kell elhelyezni [10].

Iw / d Iw = Türes / dT, ahol d Iw = Iw_terhelt – Iw és dT = Tterhelt - Türes                   (5.1)

A súrlódási erő (rv) kis értékre lett becsülve, amit bizonyára tovább lehetne vizsgálni, mint ahogy a “cogging” nyomatékból származó indítónyomaték hullámzást is. Ezen hibák a szabályozó nagyobb kitéréseit okozzák. 

8. Verzionálás, működtetés

A szoftver elérhető és működtethető az alábbiak szerint: 

>git clone https://github.com/ballonwheel/ballonwheel.git

>cd ballonwheel/bash_solution_only_octave

>sudo ./run.sh

>sudo ./stop.sh

9. Következtetések

A kifejlesztésre került eszköz jól használható kiállításokon irányítástechnikai demonstrációs célra valamint szakmai gyakorlati órákra a fejlesztés különböző lépései a modellalkotás, szabályozó tervezés és megvalósítás, hangolás, motor identifikáció és motor hajtás ismereteinek elsajátítására. A kialakított rendszer esetleg alapja lehet egy asztali, kisebb változat is vagy “DIY” egységcsomag amely motiváló lehet a diákok számára.

10. Referenciák

[1] Control of the Ball on the Wheel System, R.W. van Gils, DCT 2007.010.

Technische Universiteit Eindhoven, Department Mechanical Engineering,

Dynamics and Control Technology Group, Eindhoven, February, 2007

[2] Lindert, Sven & Höfler, Christian & Schlacher, Kurt. (2018). Nichtlineare

Regelung mit einem Raspberry PI: Automatisierung des Versuchsaufbaus ,,Ball 

auf Rad“ mit einem Raspberry PI und offener Hard- und Software. e & i 

Elektrotechnik und Informationstechnik. 135., 10.1007/s00502-018-0613-8.

[3] Keviczky, Szabályozástechnika, Szent István Egyetem, Győr

[4] Lantos Béla, Irányítási rendszerek tervezése, 11. Szabályozások tervezése 

állapottérben

[5] Openeering, LQ, Online:

http://www.openeering.com/sites/default/files/Inverted_Pendulum.pdf

[6] Matlab, Online:

https://www.mathworks.com/help/control/ref/pidtuner-app.html

[7] Octave, Instrumentation tool, Online:

https://octave.sourceforge.io/instrument-control/package_doc/

[8] Arduino cli: Online: https://arduino.github.io/arduino-cli/0.35/

[9] Halász sándor, Villamos hajtások, ISBN 963 450 5171, (7.14)

[10] Gilber, Sólyom, Kocsányi, „Merev testek kinematikai leírása,” Fizika

Mérnököknek, Műegyetemi kiadó

[11] Octave, symbolic, Online: https://octave.sourceforge.io/symbolic/

[12] Repülőgépek egyszerű referenciajel követő szabályozóinak tervezése

LQ Servo módszerrel, Matlab/Simulink környezetben, Bauer Péter

BME Közlekedésautomatikai Tanszék

[13] RTAI, Online: https://www.rtai.org/

11. Melléklet

Irtech alapok

(vegignezni: scilab help control system CACSD osszes parancs)

(alap konyv: Keviczky)

Atv fv levezetese

Atv fv alakok

Feedback atv fv

Tipus szam

Rend szam

Mit abrazol az S plane, mit lehet leolvasni rola?

Az S plane-bol hogyan lehet kovetkeztetni a rendszer viselkedesere, pl jobb oldali komplex zerus?

Bode, bode sketch

Nyquist, sketch

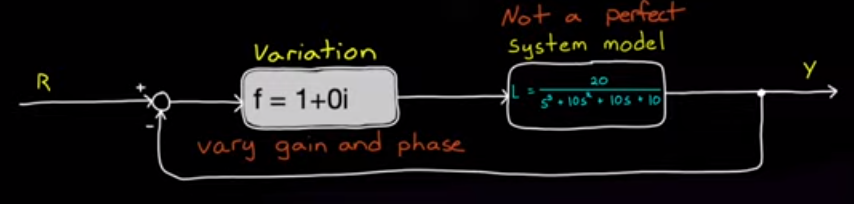
Es mekkora beavatkozo jelet kell alkalmaznom?

Es hova erdemes athelyezni a polusokat?

Gyokhely gorbe, Root locus avagy evans

Root locus sketch

PID stabil tervezes

PID instabil tervezes

Robosztus tervezes

—

Atv fv

Atviteli fv = kimenet / bemenet

A DIRAC deltara adott valaszt a sulyfv w(t)

Az egysegugrasra adott valasz az atmeneti fv v(t)

Keviczky 59.oldal, zerus, polus alak k(s-z1)(s-z2)/(s-p1)(s-p2)

Idoallandos alak: 1+ts/1+sT

S plane

https://youtu.be/CRvVDoQJjYI?list=PLUMWjy5jgHK3-ca6GP6PL0AgcNGHqn33f&t=465

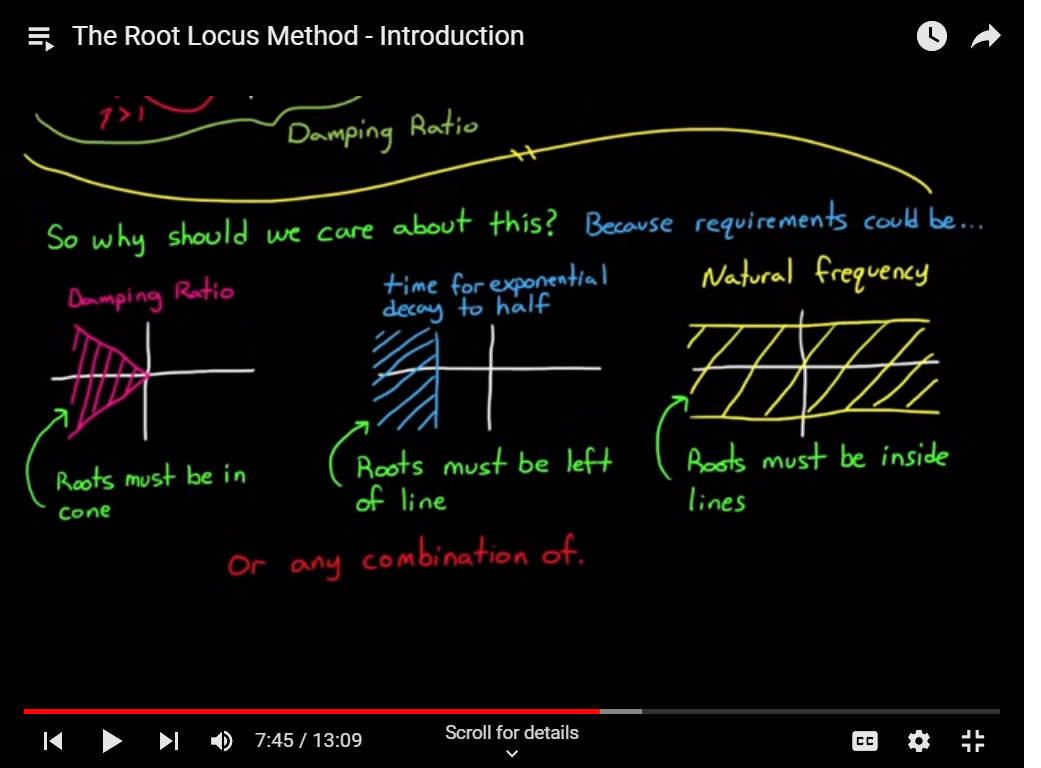
A rendszer sajat valasza, stabilitas az atv fv nevezoje, polusai, energiatarolokhoz kotodnek, nem fugg a gerjesztestol. Ahany energiatarolo, annyi fokszam. Egy tarolo nem leng, csak 2 vagy tobb. Tehat egy polus csak valos lesz, ketto lehet komplex.

A gerjesztesektol fuggo valasz a zerusokhoz, a szamlalo gyokeihez tartoznak.

Az S plane a karakterisztikus egyenletek (szamlalo, zerusok es a nevezo, polusok) gyokeinek abrazolasara komplex sikon, e^delta+-jw. Az S plane fuggoleges tengejen az jw van, tehat minnel tavolabb, annal nagyobb a lengesi freki; a vizszintes tengelye a delta a decay, lecsenges, minnel balrabb a nullatol, annal hamarabb lecseng, nullanal kvasistacionariusban leng, minnel jobrabb annal gyorsabban elszallo erosodo gerjedes.

Ha az S plane jobb oldalon van komplex zerus, akkor egysegugrasra lengo valasz, ugy, hogy ellenkezo elojelu is lesz a valasz, mig elindul a beallas fele.

A jobb oldali zero, nem minimum fazisu rendszert jelent, mert egyebkent a minimum fazisu rendszernel egy adott amplitudo gorbehez adott fazis ertek tartozik, de a nem minimum fazisunal a jobb oldali zerus, vagy a time delay hatarozza meg a hozza tartozo fazist, ami kisebb mint a min fazis es akarmennyi is lehet, “Brian D What Are Non-Minimum Phase Systems? | Control Systems in Practice “:https://www.youtube.com/watch?v=jGEkmDRsq_M&list=PLn8PRpmsu08pFBqgd_6Bi7msgkWFKL33b&index=6

Ha komplex jobb oldali zerus van, akkor a beavatkozo jel hatasara, elobb lengeni fog a kimenet, majd indul a beallas fele.

Zerus hatasara rendszer gyosithato

Zerust nem lehet polus nelkul bevezetni

A zerusokhoz pozitiv, a polusokhoz negativ monoton novekvo/emelkedo fazisszog tartozik, Keviczky, 83.oldal, zerusok hatasa

Ruth Hurwitz stabilitas tesztelni jo, de labilis rendszerhez jo a Nyquist stabilitas vizsgalatKeviczky 177.oldal

Jobb oldali labilis polust kiejteni nem szabad, nem megfigyelheto, meg iranyithato lesz; altalanositott nyquist stabilitas kell, ora jarasaval ellentetes 1szer (1 jobb polus eseten) -1et kerulni a szabalyozo+szakasz openloopnak

Root Locus

• Evans, Walter R. Evans, https://en.wikipedia.org/wiki/Root_locus_analysis

• A zart hurok stablitas vizsgalata egy parameterre nezve

• Matlabban hogyan? Teszt (GEG)

• Scilabban hogyan? Teszt (GEG)

• Kivalasztani a parametert,

  • Peldaul damping ratio

  • Vagy hurok erosites

• Rendezni az egyenltet: https://youtu.be/eTVddYCeiKI?t=299

  • Matlab a visszacsatolo agba teszi a parametert https://youtu.be/eTVddYCeiKI?t=237

    • De nem lenyeges, mert a nevezu ua

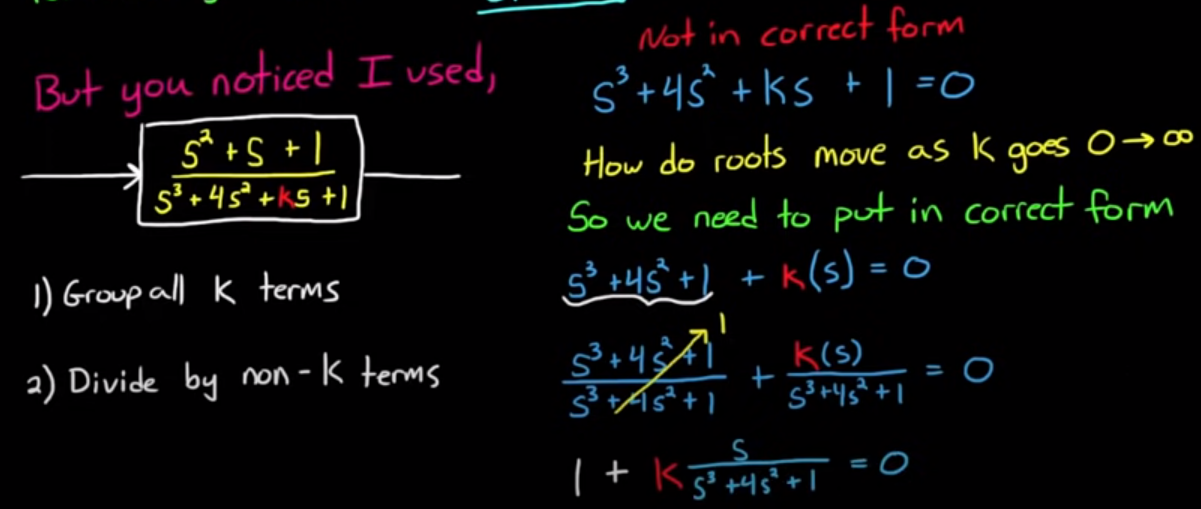
• Venni a zart hurok karakterisztkus egyenletet, tehat a nevezot – > 1+K*G(s)=0, ahol G(s)=z(s)/p(s), open loop zerusai, polusai-t abrazolni K tart 0->oo vegtelenbe

• Sketch

  • 1,

  • 2,

  • 3

  • 4

  • 5

  • 6

  • 7

  • 8

  • 9

  • 10

Nem minimum fazisu rendszerek

https://www.youtube.com/watch?v=jGEkmDRsq_M&list=PLn8PRpmsu08pFBqgd_6Bi7msgkWFKL33b&index=7

Time delay - distorting (phase shift) delay / non-distorting(transport,ideal,unit,latency) delay

https://www.youtube.com/watch?v=wouhREkqZa0&t=0s

Filter

Notch, savzaro https://www.youtube.com/watch?v=tpAA5eUb6eo&t=0s

Feedforward

https://www.youtube.com/watch?v=FW_ay7K4jPE&list=PLn8PRpmsu08pFBqgd_6Bi7msgkWFKL33b&index=3

Robosztussag

https://www.youtube.com/watch?v=b_8v8scghh8&list=PLn8PRpmsu08pFBqgd_6Bi7msgkWFKL33b&index=8

LQR

https://en.wikipedia.org/wiki/Linear%E2%80%93quadratic_regulator

https://en.wikipedia.org/wiki/Optimal_control

Model Predictive Control

https://en.wikipedia.org/wiki/Model_predictive_control

The main advantage of MPC is the fact that it allows the current timeslot to be optimized, while keeping future timeslots in account. This is achieved by optimizing a finite time-horizon, but only implementing the current timeslot and then optimizing again, repeatedly, thus differing from a linear–quadratic regulator (LQR). Also MPC has the ability to anticipate future events and can take control actions accordingly. PID controllers do not have this predictive ability. MPC is nearly universally implemented as a digital control, although there is research into achieving faster response times with specially designed analog circuitry.^[3]

Generalized predictive control (GPC) and dynamic matrix control (DMC) are classical examples of MPC.^[4]

MPC vs. LQR

Model predictive control and linear-quadratic regulators are both expressions of optimal control, with different schemes of setting up optimisation costs.

While a model predictive controller often looks at fixed length, often graduatingly weighted sets of error functions, the linear-quadratic regulator looks at all linear system inputs and provides the transfer function that will reduce the total error across the frequency spectrum, trading off state error against input frequency.

Due to these fundamental differences, LQR has better global stability properties, but MPC often has more locally optimal[?] and complex performance.

The main differences between MPC and LQR are that LQR optimizes across the entire time window (horizon) whereas MPC optimizes in a receding time window,^[4] and that with MPC a new solution is computed often whereas LQR uses the same single (optimal) solution for the whole time horizon. Therefore, MPC typically solves the optimization problem in a smaller time window than the whole horizon and hence may obtain a suboptimal solution. However, because MPC makes no assumptions about linearity, it can handle hard constraints as well as migration of a nonlinear system away from its linearized operating point, both of which are major drawbacks to LQR.

This means that LQR can become weak when operating away from stable fixed points. MPC can chart a path between these fixed points, but convergence of a solution is not guaranteed, especially if thought as to the convexity and complexity of the problem space has been neglected.

Brian Douglas, Matlab, Understanding PID control

What Is PID Control? | Understanding PID Control, Part 1

Anti-windup for PID control | Understanding PID Control, Part 2

Noise Filtering in PID Control | Understanding PID Control, Part 3

A PID Tuning Guide | Understanding PID Control, Part 4

3 Ways to Build a Model for Control System Design | Understanding PID Control, Part 5

Manual and Automatic PID Tuning Methods | Understanding PID Control, Part 6

Important PID Concepts | Understanding PID Control, Part 7

Brian Douglas matlab practical controls

What Control Systems Engineers Do | Control Systems in Practice

What Is Gain Scheduling? | Control Systems in Practice

What Is Feedforward Control? | Control Systems in Practice

Why Time Delay Matters | Control Systems in Practice

A Better Way to Think About a Notch Filter | Control Systems in Practice

What Are Non-Minimum Phase Systems? | Control Systems in Practice

4 Ways to Implement a Transfer Function in Code | Control Systems in Practice

The Gang of Six in Control Theory | Control Systems in Practice

The Step Response | Control Systems in Practice

Nichols Chart, Nyquist Plot, and Bode Plot | Control Systems in Practice

Passivity-Based Control to Guarantee Stability | Control Systems in Practice

Why Padé Approximations Are Great! | Control Systems in Practice

What are Transfer Functions? | Control Systems in Practice

Everything You Need to Know About Control Theory

Brian D, matlab, introduction to state space eq

Introduction to State-Space Equations | State Space, Part 1

What is Pole Placement (Full State Feedback) | State Space, Part 2

A Conceptual Approach to Controllability and Observability | State Space, Part 3

What Is Linear Quadratic Regulator (LQR) Optimal Control? | State Space, Part 4

Brian D, matlab, robust control

What Is Robust Control? | Robust Control, Part 1

Understanding Disk Margin | Robust Control, Part 2

Disk Margins for MIMO Systems | Robust Control, Part 3

Working with Parameter Uncertainty | Robust Control, Part 4

H Infinity and Mu Synthesis | Robust Control, Part 5

H infinity Controller Design In Matlab Simulink

Control Bootcamp: Sensitivity and Complementary Sensitivity (Part 2)

Control Bootcamp: Loop shaping

Control Bootcamp: Sensitivity and Robustness

Control Bootcamp: Limitations on Robustness

Robust - handling uncertinity

Gain and phase margin meghatarozasa

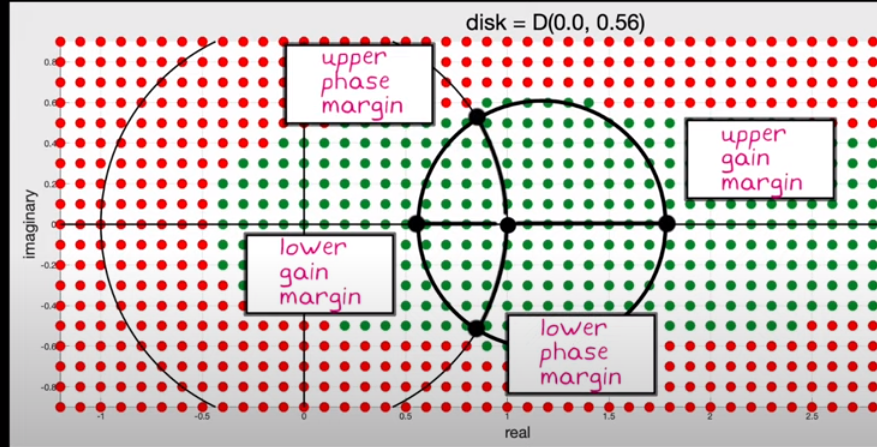
Brian D, matlab, system identification

What Is System Identification? | System Identification, Part 1

Linear System Identification | System Identification, Part 2

Nonlinear System Identification | System Identification, Part 3

Online and Recursive System Identification | System Identification, Part 4

Brian D , Matlab, learning base control

What is Extremum Seeking Control? | Learning-Based Control, Part 1

Constraint Enforcement for Improved Safety | Learning-Based Control, Part 2

What Is Model Reference Adaptive Control (MRAC)? | Learning-Based Control, Part 3

Brian D , Matlab, reinforcement learning

What Is Reinforcement Learning?

Reinforcement Learning for Engineers, Part 2: Understanding the Environment and Rewards

Reinforcement Learning Policies and Learning Algorithms

Solving the Walking Robot Problem with Reinforcement Learning

Overcoming the Practical Challenges when using Reinforcement Learning

Introduction to Multi-Agent Reinforcement Learning

Why Choose Model-Based Reinforcement Learning?

linearization

Trimming and Linearization, Part 1: What Is Linearization?

Trimming and Linearization, Part 2: The Practical Side of Linearization

Brian D, matlab tech talks , other

Understanding the Z-Transform

Brian Douglas video:

Control System Lectures - Bode Plots, Introduction

Bode Plots by Hand: Real Constants

Bode Plots by Hand: Poles and Zeros at the Origin

Bode Plots by Hand: Real Poles or Zeros

Bode Plots by Hand: Complex Poles or Zeros

CORRECTION: Bode Plots by Hand: Complex Poles or Zeros

Designing a Lead Compensator with Bode Plot

Designing a Lag Compensator with Bode Plot

Discrete control #1: Introduction and overview

Discrete control #2: Discretize! Going from continuous to discrete domain

Discrete control #3: Designing for the zero-order hold

Discrete control #4: Discretize with the matched method

Discrete control #5: The bilinear transform

Discrete control #6: z-plane warping and the bilinear transform

The Root Locus Method - Introduction

Sketching Root Locus Part 1

Sketching Root Locus Part 2

Designing a Lead Compensator with Root Locus

Designing a Lag Compensator with Root Locus

Root Locus Plot: Common Questions and Answers

Gain a better understanding of Root Locus Plots using Matlab

Routh-Hurwitz Criterion, An Introduction

Routh-Hurwitz Criterion, Special Cases

Routh-Hurwitz Criterion, Beyond Stability

other

Drone Control and the Complementary Filter

Where have I been?

A real control system - how to start designing

Standard HW Problem #2: Which is the real open loop transfer function?

Simplifying and modifying block diagrams

Transfer Functions: Putting it all together

The Laplace Transform - A Graphical Approach

Why Use Kalman Filters? | Understanding Kalman Filters, Part 1

State Observers | Understanding Kalman Filters, Part 2

Optimal State Estimator | Understanding Kalman Filters, Part 3

Optimal State Estimator Algorithm | Understanding Kalman Filters, Part 4

Nonlinear State Estimators | Understanding Kalman Filters, Part 5

How to Use a Kalman Filter in Simulink | Understanding Kalman Filters, Part 6

How to Use an Extended Kalman Filter in Simulink | Understanding Kalman Filters, Part 7

Neso Academy

Control Systems

/***********/

oldal1-RLC

/***********/

openeering,

scilabninja,

Keviczky

https://www.mikrocontroller.net/attachment/341426/Understanding_digital_signal_processing.pdf

https://www.youtube.com/watch?v=wkfEZmsQqiA&list=PLBFsvLJJNYJ2K0Kt2ULF5-0eLXavhQB5i

https://www.youtube.com/watch?v=ApMz1-MK9IQ&list=PLn8PRpmsu08pFBqgd_6Bi7msgkWFKL33b

https://www.youtube.com/watch?v=Z1QS6FsxrJI&list=PLn8PRpmsu08p5KkY8_P8G6fJhelUHHi6b

https://www.youtube.com/watch?v=A7wHSr6GRnc&list=PLn8PRpmsu08qFLMfgTEzR8DxOPE7fBiin

https://github.com/aerojunkie/control-tools

ertekezes szeruen hasznosabb lenne, mert erthetobb a gondolkodas menete, pl: A zerusok a gerjesztesekhez tartozank, a polusok a sajatvalaszhoz. A polusoktol fugg, hogy milyen valaszt ad a rendszer, ha gerjesztest kap es utana mi lesz…insabil, ha jobb oldali a S plane- ami a nevezo karakterisztikus egyenletenek megoldasai---ahol a polus = nulla, aza szakadasa van az atvfv-nek, tehat nem ertelmezett. (?)

resFilter, bandpass

altalaban veve a high, lowpass difftag +20dB/D es +90deg; inttag -20db/D es -90deg; w0-on a ketto kozotti atmenet

quadratic kimenet: a diff reszben +270deg ??? ez mit is jelent??

DerFilt

phase lag/lead , notch

/***********/

oldal2-motorRL, 95.oldal megtanulni, csinalni ra PIDet, 8.5fejezet, 251.oldal, labilis szabalyozasok

/***********/

https://ctms.engin.umich.edu/CTMS/index.php?aux=Home

/***********/

oldal3-mech

/***********/

https://ctms.engin.umich.edu/CTMS/index.php?aux=Home

/***********/

oldal4-bow

/***********/

4,1, modell lagrange/newton

4,2 ABCD

4,3 polezero map

4,4 K à poleplace / LQ à lasd lent!!!

4,5 polezero map

4,6 discretizacio

4,7 polezero map

4,8 robosztussag hatarai: diszkretizacio, LQsulyok, polezeroHol, pospontossag, cooggingTorwue, csuszas, tapfeszNagysag, taőfesz felbontas, tapugrasgyorsasag, homerseklez(R, L, pos, delta_voltage)

/***********/

oldal5-invertedinga

/***********/

POLUSKIEJTES

szimmetrikal optimum, technikal optimum

POLUS ATHELYEZES

Keviczky 277oldal eleg kurta

https://ctms.engin.umich.edu/CTMS/index.php?example=InvertedPendulum&section=ControlStateSpace#6

https://eng.libretexts.org/Bookshelves/Industrial_and_Systems_Engineering/Book%3A_Introduction_to_Control_Systems_(Iqbal)/09%3A_Controller_Design_for_State_Variable_Models/9.01%3A_Controller_Design_in_Sate-Space

106., 127. oldal szerint bow vizsgalat

hol vannak a polusok? https://help.scilab.org/trfmod

hova helyezzuk at? (lasd matlab fent: minnel tavolabb, a gain is csokken)https://help.scilab.org/ppol

hogyan ejtesz ki jobb oldali zero-t -->nem min fazis rendszer, step-re eloszor ellentetes iranyba megy? (ha megfigyelheto es vloszinu, hogy nem konjugalt komplex, hanem csak valos resze van, de ez nem kotelezo)

àbal oldali zerusokkal, de az bal oldali polust is behoz

àallapotvcsvel, de a K onmagaban nem szedi ki, hanem az ’u’ elotti offszet eltolassal valoszinu, hogy ki lehet

--> kiejteni nem jo otlet jobb oldali polusokkal, instabil; a legegyszerubb legjobb, h a system gain csokkentes, lassitani a reakciot, lassabb lesz a beallas, de van ideje reagalni a rendszernek, nem gerjed be

https://www.youtube.com/watch?v=jGEkmDRsq_M&t=3s

https://math.stackexchange.com/questions/2598750/what-is-the-significance-of-unstable-zeros-in-control-system

Additionally, zeros cannot be be moved by feedback, the way poles can be assigned. Zeros with nonnegative real part cannot be canceled, because the cancellation would be unstable. Thus the designed has to live with them, as a fundamental limitation on our ability to design a feedback controller. (I should add that time-domain linear quadratic control is of limited use in understanding the role of zeros.)

++

megcsinalni, hogy az Splane polus athelyezes hogyan hat a beavatkozo jel kondiciokra: max u es max_du/dt ßez vhol benne van a brain douglas videokban!!

https://web.mit.edu/2.14/www/Handouts/PoleZero.pdf

--------------------

zerusok hatasai:

nyq 0bol +jbe tarto

bode amp +20db

bode ph vagasnal +90be

bal oldali zerussal a rendszer gyorsithato

zerust csak polussal egyutt lehet realizalni

85oldal fazis kesleteto sieteto tag

--

idotarolos alakbol bal/jobb stabil/labilis megallapithato

y=be/ki=(1+sT1)/(1+sT2), ha +, akkor stabil, tehat bal oldali akar zerus(szamlalo) akar polus(nevezo)

--

bodeph: bode-amplitudo-hoz egyertelmuen kotheto, mert

baloldali polus stabilis neg szog tartozik

baloldali zerus stabilis poz szog à min fazisu

jobboldali polus labilis poz bodeph

jobboldali zerus labilis neg bodeph à ezert ez a NEM minimum fazisu

**********

polus athelyezes hogyanok:

https://ctms.engin.umich.edu/CTMS/index.php?example=InvertedPendulum&section=ControlStateSpace#6

LQ 16.oldal

http://www.openeering.com/sites/default/files/Inverted_Pendulum.pdf

matlab, place()

https://ctms.engin.umich.edu/CTMS/index.php?example=Introduction&section=ControlStateSpace

https://de.mathworks.com/help/control/ref/place.html

Diszkret integrator

https://www.mathworks.com/help/simulink/slref/discretetimeintegrator.html

Output Equations

With the first time step, block state n = 0, with either initial output y(0) = IC or initial state x(0) = IC, depending on the Initial condition setting parameter value.

For a given step n > 0 with simulation time t(n), Simulink® updates output y(n) as follows:

Forward Euler method:

y(n) = y(n-1) + K*[t(n) - t(n-1)]*u(n-1)

Backward Euler method:

y(n) = y(n-1) + K*[t(n) - t(n-1)]*u(n)

Trapezoidal method:

y(n) = y(n-1) + K*[t(n)-t(n-1)]*[u(n)+u(n-1)]/2

Simulink automatically selects a state-space realization of these output equations depending on the block sample time, which can be explicit or triggered. When using explicit sample time, t(n)-t(n-1) reduces to the sample time T for all n > 0.

Integration and Accumulation Methods

This block can integrate or accumulate a signal using a forward Euler, backward Euler, or trapezoidal method. Assume that u is the input, y is the output, and x is the state. For a given step n, Simulink updates y(n) and x(n+1). In integration mode, T is the block sample time (delta T in the case of triggered sample time). In accumulation mode, T = 1. The block sample time determines when the output is computed but not the output value. K is the gain value. Values clip according to upper or lower limits.

Forward Euler Method

Forward Euler method (default), also known as forward rectangular, or left-hand approximation

The software approximates 1/s as T/(z-1). The expressions for the output of the block at step n are:

x(n+1) = x(n) + K*T*u(n)

y(n) = x(n)

The block uses these steps to compute the output:

Step 0: y(0) = IC (clip if necessary)

x(1) = y(0) + K*T*u(0)

Step 1: y(1) = x(1)

x(2) = x(1) + K*T*u(1)

Step n: y(n) = x(n)

x(n+1) = x(n) + K*T*u(n) (clip if necessary)

Using this method, input port 1 does not have direct feedthrough.

Backward Euler Method

Backward Euler method, also known as backward rectangular or right-hand approximation

The software approximates 1/s as T*z/(z-1). The resulting expression for the output of the block at step n is

y(n) = y(n-1) + K*T*u(n).

Let x(n) = y((n)-1). The block uses these steps to compute the output.

If the parameter Initial condition setting is set to Output or Auto for triggered and function-call subsystems:

Step 0: y(0) = IC (clipped if necessary)

x(1) = y(0)

If the parameter Initial condition setting is set to Auto for non-triggered subsystems:

Step 0: x(0) = IC (clipped if necessary)

x(1) = y(0) = x(0) + K*T*u(0)

Step 1: y(1) = x(1) + K*T*u(1)

x(2) = y(1)

Step n: y(n) = x(n) + K*T*u(n)

x(n+1) = y(n)

Using this method, input port 1 has direct feedthrough.

Trapezoidal Method

For this method, the software approximates 1/s as T/2*(z+1)/(z-1).

When T is fixed (equal to the sampling period), the expressions to compute the output are:

x(n) = y(n-1) + K*T/2*u(n-1)

y(n) = x(n) + K*T/2*u(n)

If the parameter Initial condition setting is set to Output or Auto for triggered and function-call subsystems:

Step 0: y(0) = IC (clipped if necessary)

x(1) = y(0) + K*T/2*u(0)

If the parameter Initial condition setting is set to Auto for non-triggered subsystems:

Step 0: x(0) = IC (clipped if necessary)

y(0) = x(0) + K*T/2*u(0)

x(1) = y(0) + K*T/2*u(0)

Step 1: y(1) = x(1) + K*T/2*u(1)

x(2) = y(1) + K*T/2*u(1)

Step n: y(n) = x(n) + K*T/2*u(n)

x(n+1) = y(n) + K*T/2*u(n)

Here, x(n+1) is the best estimate of the next output. It is not the same as the state, in that x(n) is not equal to y(n).

Using this method, input port 1 has direct feedthrough.

When T is a Variable

WhenT is a variable (for example, obtained from the triggering times), the block uses these steps to compute the output.

If the parameter Initial condition setting is set to Output or Auto for triggered and function-call subsystems:

Step 0: y(0) = IC (clipped if necessary)

x(1) = y(0)

If the parameter Initial condition setting is set to Auto for non-triggered subsystems:

Step 0: x(0) = IC (clipped if necessary)

x(1) = y(0) = x(0) + K*T/2*u(0)

Step 1: y(1) = x(1) + K*T/2*(u(1) + u(0))

x(2) = y(1)

Step n: y(n) = x(n) + K*T/2*(u(n) + u(n-1))

x(n+1) = y(n)

Discrete time derivative

DEEP LEARNING

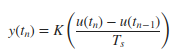
https://www.youtube.com/watch?v=PqDwddEHswU&list=PLn8PRpmsu08ol7qVBak-RUKrBNkn3H58R

FUZZY

https://www.youtube.com/watch?v=__0nZuG4sTw&list=PLn8PRpmsu08pSpYcLLkfXcYlcs5judk0d

What Is Fuzzy Logic? | Fuzzy Logic, Part 1

Fuzzy Inference System Walkthrough | Fuzzy Logic, Part 2

Fuzzy Logic Examples | Fuzzy Logic Part 3

Fuzzy Logic Controller Tuning | Fuzzy Logic, Part 4

12. Ballonwheel project install

1, Linux rt kernel install

5.15.32-v8+

5.15.36-rt41-v8+

git install

2, git clone

imre@raspberrypi:~ $ git clone https://github.com/ballonwheel/ballonwheel.git

Cloning into 'ballonwheel'...

remote: Enumerating objects: 243, done.

remote: Counting objects: 100% (89/89), done.

remote: Compressing objects: 100% (55/55), done.

remote: Total 243 (delta 61), reused 61 (delta 33), pack-reused 154

Receiving objects: 100% (243/243), 245.77 KiB | 3.84 MiB/s, done.

Resolving deltas: 100% (146/146), done.

>sudo apt-get install octave

>sudo apt-get install octave-control

>sudo apt-get install octave-signalcd

3, arduino cli install

https://github.com/arduino/arduino-cli/releases

mkdir /home/imre/bow

cd bow

wget https://github.com/arduino/arduino-cli/releases/download/0.22.0/arduino-cli_0.22.0_Linux_64bit.tar.gz

Kicsomagol ide

imre@raspberrypi:~/bow $ tar -xf arduino-cli_0.29.0_Linux_ARM64.tar.gz

./arduino-cli core install arduino:avr // → avr telepites

4, ../../bow/arduino-cli compile --verbose --fqbn arduino:avr:nano arduino.ino

Lehet ez internet nelkul? Mert ugy tunik, hogy csak online megy, mert auto update van…

5, #sudo chmod 777 /dev/ttyUSB0

6, ../../bow/arduino-cli upload -v -p /dev/ttyUSB1 --fqbn arduino:avr:nano arduino.ino

>df -haT

Filesystem Type Size Used Avail Use% Mounted on

/dev/root ext4 7.1G 2.9G 4.0G 42% /

7, ez akkor kell, ha git push van

imre@thinkpad:~/.ssh$ sudo scp -v id_ed25519.rsa imre@192.168.1.11:~/

8,

imre@thinkpad:~/.ssh$ sudo scp -v id_ed25519.rsa.pub imre@192.168.1.11:~/

9,

imre@raspberrypi:~ $ mkdir .ssh

imre@raspberrypi:~ $ mv id_ed25519.rsa .ssh/

imre@raspberrypi:~ $ mv id_ed25519.rsa.pub .ssh/

imre@raspberrypi:~ $ chmod 755 .ssh/

imre@raspberrypi:~ $ cd .ssh/

imre@raspberrypi:~/.ssh $ chmod 600 id_ed25519.rsa

10,

imre@raspberrypi:~ $ eval "$(ssh-agent -s)"

Agent pid 12933

imre@raspberrypi:~ $ ssh-add .ssh/id_ed25519.rsa

Enter passphrase for .ssh/id_ed25519.rsa:

Identity added: .ssh/id_ed25519.rsa (dobany.hu@gmail.com)

11,

imre@raspberrypi:~ $ cd ballonwheel/

imre@raspberrypi:~/ballonwheel $ git status

On branch main

Your branch is up to date with 'origin/main'.

nothing to commit, working tree clean

imre@raspberrypi:~/ballonwheel $ git config --global user.name "imre from raspZero_1"

imre@raspberrypi:~/ballonwheel $ git commit -a

[main 7db3bc0] teeszt

1 file changed, 1 insertion(+), 1 deletion(-)

12,

https://docs.github.com/en/get-started/getting-started-with-git/managing-remote-repositories

imre@raspberrypi:~/ballonwheel $ git remote set-url origin git@github.com:ballonwheel/ballonwheel.git

imre@raspberrypi:~/ballonwheel $ git remote -v

origin git@github.com:ballonwheel/ballonwheel.git (fetch)

origin git@github.com:ballonwheel/ballonwheel.git (push)

imre@raspberrypi:~/ballonwheel $ git push

The authenticity of host 'github.com (140.82.121.4)' can't be established.

ECDSA key fingerprint is SHA256:p2QAMXNIC1TJYWeIOttrVc98/R1BUFWu3/LiyKgUfQM.

Are you sure you want to continue connecting (yes/no/[fingerprint])? yes

Warning: Permanently added 'github.com,140.82.121.4' (ECDSA) to the list of known hosts.

Enumerating objects: 5, done.

Counting objects: 100% (5/5), done.

Delta compression using up to 4 threads

Compressing objects: 100% (3/3), done.

Writing objects: 100% (3/3), 296 bytes | 42.00 KiB/s, done.

Total 3 (delta 2), reused 0 (delta 0), pack-reused 0

remote: Resolving deltas: 100% (2/2), completed with 2 local objects.

To github.com:ballonwheel/ballonwheel.git

acbe9ab..7db3bc0 main -> main

imre@raspberrypi:~/ballonwheel $

13,

imre@raspberrypi:~/ballonwheel $ sudo apt-get install setserial

14,

imre@raspberrypi:~/ballonwheel $ sudo setserial -v /dev/ttyUSB0 low_latency

/dev/ttyUSB0, UART: unknown, Port: 0x0000, IRQ: 0, Flags: low_latency

15,

imre@raspberrypi:~/ballonwheel $ gcc -v -pthread main.c

16.

>sudo octave

>pkg install -verbose -forge -global control

>pkg install -verbose -forge -global signal

17.

Nano vagy vim

18

Gnuplot